实验离心技术的基本计算方法

一、一般计算

设离心转头以匀角速度ϖ在离心室中等速旋转，悬浮在离心管或转头中溶剂内的颗粒（被分离的）的密度为σ，溶剂（或梯度材料）的密度为ρ，粘性系数为η。
颗粒所在位置与旋转中心距离r,颗粒本身体积为V。根据经典的牛顿力学基本原理，质量为m的颗粒受到的离心力为：

用 N=rpm=转/分来表示

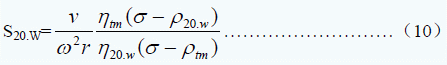
定义 RCF（相对离心场）为实际离心加速度化成重力加速度的倍数则有：

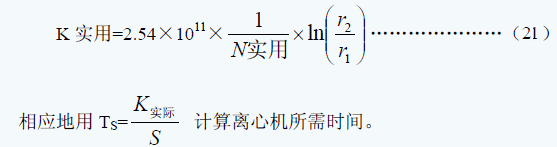
式中 g为重力加速度，（×g）表示重力加速度的倍数。式中ｒ用厘米表示。

（3）式为应用昀广的相对离心加速度公式，是离心技术中的重要技术参数。又设颗粒为球形直径为 d（厘米）（非球形颗粒计算可修正），在沉降方向受到的离心力与浮力之和为

以沉降速度 v在溶液中运动的颗粒受到流体的反向摩擦阻力为 f,根据粘性流体力学的 stokes定理：

如果颗粒以匀速沉降则 F1=f 计算简化后

定义 S为单位离心加速度的沉降速度

我们称 S为沉降系数，S值单位为秒-1，由于颗粒直径很小（微米至毫微米级） S值也很小，一般以10^-13为一个基本计算单位S，为了纪念离心技术早期（1920~1940）的奠基人Svedberg，而把 S称为 Svedberg常数。在生物学各种论文常见的某物质沉降系数为多少个 S，即指此单位。

二、各种离心方法（差分，速率一区带，等密度等）中样品颗粒的沉降行为：
分析（6）式
若 σ > ρ则 v >0, S>0, 颗粒顺离心力方向沉降。
若 σ = ρ则 v = 0, S=0,颗粒沉降或上浮到某一位置达到平衡。
若 σ < ρ则 v <0, S<0,颗粒逆离心力方向上浮。
这个简单的分析很好地解释了样品颗粒用各种离心方法分离时的沉降行为。在差分离心中，样品颗粒按照他们的密度大于或小于溶液密度而沉降（昀后变为沉淀）或上浮（变成上浮物，浮在液面）；在速率一区带离心中由于梯度液所设计的昀大密度小于样品颗粒（各种组份）密度而使混合样品中不同组份颗粒按不同沉降速度以不同纯样品区带方式沉降，而离心时间控制在昀重的样品变或沉淀之前停机，使不同组份以纯样品带方式存在于梯度液之中而达到分离纯化的目的；在等密度离心中在梯度液上部，下部或混合在梯度液中的样品各个不同组份按它们的密度不同在离心力作用下沉降或上浮到各自的等密度区（ σ = ρ ,v = 0）形成纯样品区带。
与公式（6）（离心场）对照的是在地球引力场中

比较（ 6）、（8）由于目前离心技术的进展，实验离心机所产生的离心加速度已达到重力加速度数万甚至一百多万倍（目前昀高为 105万倍），因而，与重力场的自然沉降相比，样品颗粒的沉降速度也相应加快了同样的倍数。这样就使得很多直径为微米级或更小的生物体组份可以利用各种类型的离心机在数分钟至数十小时的时间内被分离纯化，对于非球形颗粒，沉降时间可以用经验公式进行修正[见（四）部分 ].

三、在不同介质中样品沉降系数的换算

为了便于比较，将任意介质中的S统一校正到 20℃水中的S，设某个温度t某个介质m的沉降系数为S_tm

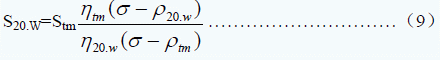
也可以表达为

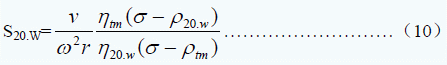
四、沉降时间计算：

（1）、一般分析

沉降时间可以对t的积分求得：

设颗粒起始位置的r_min，沉降终了位置为 r_max，从 r_min沉降到 r_max所需要的时间为：

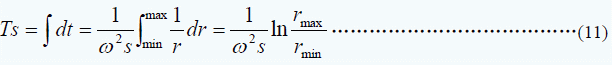
很明显如果给出了沉降时间就可以算出沉降系数：

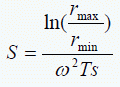
对现代离心机，ω² Ts在离心过程中可自动计算，这样计算就十分简单，针对（11）式，如果把S化为 Svedberg单位，r用厘米表示，ω化为 N（转/分）并将Ts化成小时则有

计算时要注意 S值应该是在离心温度时特定介质中的沉降系数。
对于特定转头，当转速选定后样品的初始及终了位置已定（如用差分法，样品沉降到底部）则：

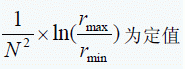
而对于选定转头，可以知道他们的最高转速为N，于是，定义K为转子常数

目前在离心机转头说明书上都列出了转子的 K值，它是指在该转子昀高转速运转时，根据转子几何尺寸定下的 rmax和 rmin算出的，K值越小对同一样品离心时间越短。
比较（12）、（13）式：

这个简单公式常用于估算离心时间。式中 S可由计算算出也可按文献中以测定类似物的估计值算出。
如果我们不选用该转头昀高转速而用一个实际转速，则有：

对同一样品在不同K值时沉降时间：

（14）式中S是对球形颗粒计算出的，对非球形颗粒，沉降中受到的流体阻力较大（沉降中非球形颗粒是无规则悬浮在离心介质中）。
假设我们计算中采用的是球形样品的计算值，我们可以把非球形样品简化成长、段半径之比为C的椭球体，而椭球体的沉降时间与球体沉降时间Ts之间关系可表达为

k与 c的关系按经验公式列出

（2）等密度离心的沉降时间计算

（Ⅰ）自形成梯度（平衡等密度离心）离心时间计算
在这类离心中样品和梯度液混合，离心过程中梯度液在离心力作用下形成密度梯度，与此同时，样品中各个组份沉降或上浮，向自己的等密度区靠拢昀后形成纯样品区带，这样的离心所需时间为

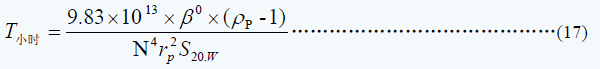
式中： N：实际转速（转/分）
           ρ_P 样品需要达到的密度
           r_p从旋转轴心沉降到等密度带的距离 
           β⁰：取决于梯度材料及溶液初始密度的常系数（β⁰值参见文献 4）

计算举例： 
设：某种天然DNA的 CsCI平衡等密度离心（自形成梯度）
初始密度：1.70克/厘米³，据参考文献查出β⁰=1.14×10⁹
样品S_{（20，W）⁼}9， N=40,000(转/分) 
选用某甩平转头r_p=10厘米，ρ_P =1.71克/厘米³

于是：

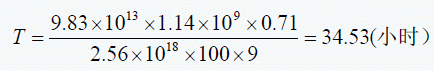
若转速降为 35000转/分，T=58.9（小时）
若使用某近垂直管转头，并在CsCI中加 E.B及Triton-X100则初始密度为1.55克/厘米³，选用转速 78000转/分，可以算出T=4（小时)．
如改用某个垂直管转头，N=100,000转/分
可算出 T=1.83小时（约等于1小时 50分）．

（Ⅱ）予形成梯度的沉降时间计算
浮在梯度液上表面的样品在离心力作用下穿过梯度层到达其等密度线上沿所用时间为（小时）：

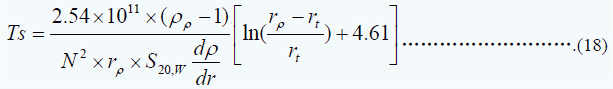
式中：r_t梯度试验液上表面到旋转中心距离（厘米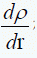）、 梯度在r处斜率，其他符号含义同（17）

计算举例：

设：甩平转头，N=30,000转/分，ρ_r =1.70克/厘米3，r_p=10厘米，r_t=6.4厘米。

则有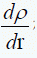： = 0.36 （梯度线倾角 20°）

         S20W=15 
代入，T=14.7（小时）
若改用某垂直管转头：N=90000转/分，r_ρ=6.6厘米， r_t=6厘米其他条件不变可算出T=1.42小时（约为 1小时 25分）

（18）式也可以用于计算速率一区带密度梯度离心所需时间。只是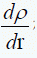 =常数，即梯度为线性或近似线性分布r_ρ为样品到达某一预期密度(ρ_ρ)处的离心的半径。

五、沉降系数的近似计算

（Ⅰ）利用速率一区带密度梯度离心作沉降系数的近似计算；
用超速（ 40000~42000转/分）细长离心管（ 10~13毫升，离心管长 9~10厘米）选用线性梯度或凸指数梯度（可以提高在较高密度区的分辨率）。

测定样品在相同的离心条件下（温度、转速、加减速速率，转头、离心管样品量，梯度材料及梯度曲线等等）以不同沉降时间离心数次，测出沉降带的位置（昀好用梯度仪抽出，经蠕动泵至带流动池的分光光度计检测某一纯样品带的位置，昀后用部分收集器收集）即可计算 S值。不同的离心时间（如 t₂,t₁），代入ω (角速度)，r为轴心至沉降面距离（厘米）、t为离心时间用分表示。
用移动界面法，分析用超速离心机或带分析附件的制备用超速离心机，从照相的纹影（schlieren）图上用比长仪测定（界面）的位置，以log r对t作图，可以求得直线斜率： 

从中算出 S值。
如果 log r－t不是直线，则可以分别求每个时间的S值然后作s-t图，并外延至t=0时的S作为计算标准。当然，S也要化成 S_20.W。

（Ⅱ）某些生物大分子的沉降系数与分子量之间关系时经验公式：

六、转子常数：在计算沉降时间公式（12）中我们曾引入转子常数K（公式 13）。离心机说明书上绘出的 K值是指该转头在昀高转速时从r_min沉降到r_max时的K值。实际上我们一般不用N实际，而沉降也往往是从某初始位置rl沉降到终了位置 r2. 
于是在这种情形中

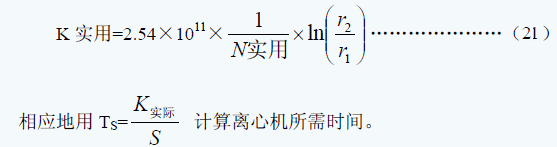
对于同类转头，K值越小，使用价值越高，在选择离心条件时有更大的余地。对不同类别的转头，由于它们的特点和用途不同，K值是衡量转头性能的一个因素。
由于转头在容量上的差异，使它们的综合利用价值不局限于K值。我们近可以引入另一个系数 L：

式中 V_R为转子各离心管名义容量的总和，用厘米³表示，同类转子的价值差异，除了材料加工等因素外还要取决于 L值，L越小，价值越高。
在欧洲还常常用Pi值来表达转子的性能

七、分子量计算：

已知沉降系数，可以用经验公式计算分子量，反之亦然［五节之（Ⅱ）］也可以用超离心法先求得沉降系数，扩散系数，再来计算分子量。
设在溶剂内悬浮的样品颗粒在离心场中有效质量为m，角速度ω，瞬时回转半径r , 沉降速度为υ，在粘性流体中匀速沉降的摩擦系数为 fo。
根据力学平衡原理：

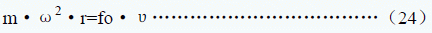
由于颗粒悬浮在溶液中设其真实质量为m_r ,σ为颗粒密度ρ为溶剂密度，于是有