图示的凸轮是一个平面凸轮,它都是由圆弧与圆弧相切组成的。用手工编制加工该凸轮的程序的主要问题是计算各切点的坐标值。在计算时,我们应首先计算各圆弧圆心的坐标值,然后求出各基点的坐标,以便于划分程序段。从图中我们可以看到,该凸轮的轮廓由四个主要圆弧及四个过渡圆弧组成,过渡圆弧的作用是使两个主要圆弧之间的连接,变成相切。这样在加工凸轮轮廓时,就不会产生过切的现象,而成为平滑曲线。
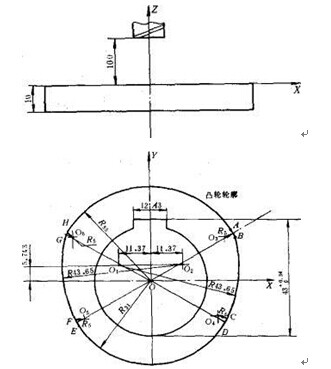
由于四处过圆弧与其它两个主要圆弧的连接是一样的,都是已知两圆和过渡圆的半径,求过渡圆与已知圆的切点。因此我们可以推导出通用的切点坐标计算公式。
设图中两已知圆的圆心分别为O1及O ,半径分别为r1及r2,过渡圆的半径为R。
由图可知,过渡圆圆心0(x0,y0)是在圆心分别为O1及O2,半径分别为R—r1及R- r2两圆的一个交点上,即过渡圆圆心坐标满足方程组
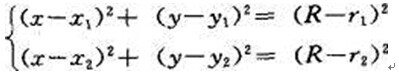
由于A是圆0及圆O1的公切点,故必在两圆的连心线上,即切点A的坐标满足方程组
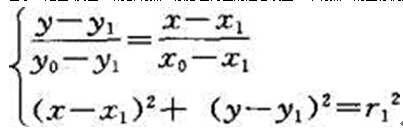
同理可得切点B的坐标满足方程
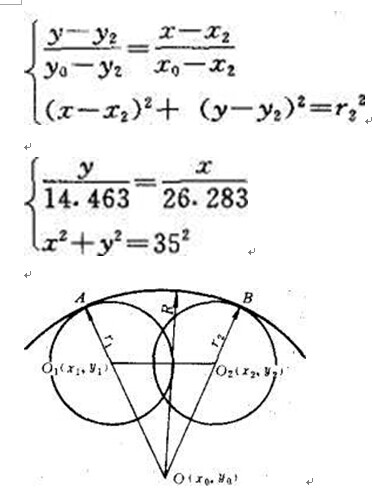
根据以上公式,我们就可以求出该凸轮各个切点的坐标值。以切点A为例,由图可知两已知圆的圆心坐标,半径和过渡圆的半径分别为x1=0 y 1=0 r 1=35 x 2=-11.37 y 2=5.743 r 2=43.65 R=5
将上述各已知数分别代入有关方程组,得过渡圆的圆心方程组
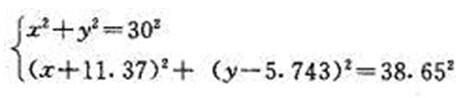
解方程组,可得过渡圆圆心0。的坐标值为 x=26.283 y=14.463
再将计算结果代入计算切点坐标的方程组
解方程组,得切点A的坐标值 x=30.668 y=16.867
同理可以求出其它点的坐标。坐标值如下
0 (21.292,-14.922) 0 (-21.292,-14.922) 0 (-26.283,14.463)
B(31.15,15.603) C(25.502,-17.628) D(25.396,-17.777)
E(-25.396,-17.777) F(-25.502,-17.628) G(-31.15,15.603)
H(-30.668,16.867)
依据以上数据进行编程,程序如下
%0003
N01 G92 X0 Y0 Z100.0
N02 G90 G00 X-35.0 Y35.0 S800 M03
N03 Z-15.0 M08
N04 G41 G01 X-10.0 Y35.0 D01 F100
N05 X0
N06 G02 X30.668 Y16.867 R35.0
N07 G02 X31.15 Y15.603 R5.0
N08 G02 X25.502 Y-17.628 R43.65
N09 G02 X25.396 Y-17.777 R5.0
N10 G02 X-25.396 Y-17.777 R31.0
N11 G02 X-25.502 Y-17.628 R5.0
N12 G02 X-31.15 Y15.603 R43.65
N13 G02 X-30.668 Y16.867 R5.0
N14 G02 X0 Y35.0 R35.0
N15 G01 X10.0
N16 G40 G00 X35.0 Y35.0 M09
N17 Z100.0
N18 X0 Y0
M05
M19 M30










 QQ交流群
QQ交流群

