国内外很多学者和研究机构都对动圈式直线电机进行了研究,但是大部分研究都集中在对永磁体的结构和材料、电机整体结构的优化、结合高效控制策略的控制电路与芯片设计等领域。而针对其力功比和从启动到稳态的时间延迟的研究还不多,本文就此部分作了深入的探讨。
动圈式直线电机可将外界输入的电压信号连续成比例地转换成往复直线运动的直线位移,并能够产生同尺寸结构2.5倍左右的电磁力,且以高线性、小滞环特性而受到广泛关注。但是传统结构的单线圈式线圈组件在运动过程中,磁性材料内部易产生涡流,使线圈产生的电磁力减小。同时由于线圈组件固有阻抗特性的限制,导致其无论在响应时间还是在响应速度上都存在一定的局限性。开发大输出电磁力和高响应的动圈式直线电机,是电工领域的发展趋势。
为此,文中提出了一种双向可逆控制的新型动圈式直线电机,针对其载流线圈采用新型线圈分割再串、并联变换组合方式,通过改变电阻和时间常数提高线圈两端的加载响应时间,采用PWM脉宽调制的控制方式对其线圈电流的大小及方向进行控制,不仅可以实现电机转换控制的稳定无扰动,而且能够实现装置的大电磁力输出和高频响应特性。
结构与原理
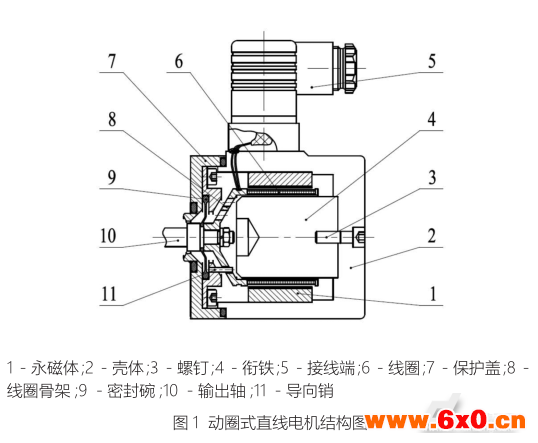
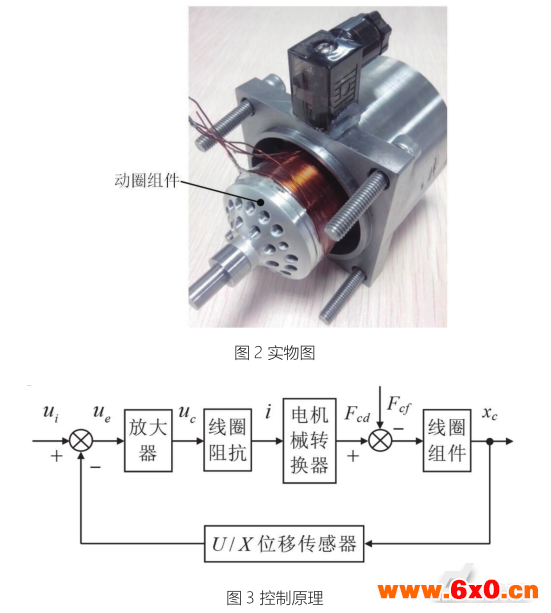
动圈式直线电机结构如图1,壳体内壁圆周上固连有若干片环形分布的瓦型永磁体,衔铁位于环形分布的永磁体内,且与壳体的一端用螺钉固连。载流线圈缠绕在电磁力线圈骨架上,并与输出轴相连,通过一导向销,浮动于永磁体与衔铁之间的气隙内,并通过密封碗与外界隔开。该新型环状动圈式直线电机实物图如图2所示。
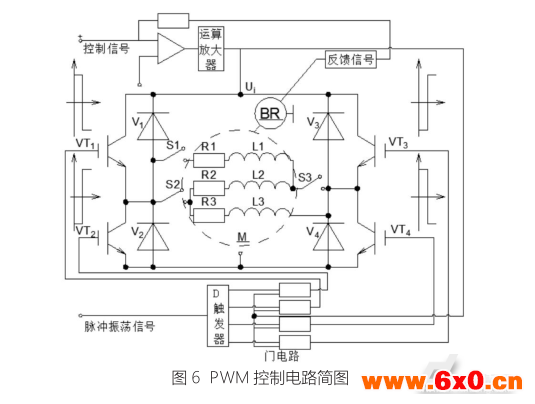
其控制原理如图3所示,首先,输入信号电压ui经放大器处理后,加载到控制线圈,载流控制线圈连同电磁力线圈骨架在永磁体提供的恒定磁场中,受电磁力Fcd作用而产生位移xc,从而带动轴芯一起运动。线圈组件由位移传感器检测位置误差,然后转换成信号电压,补偿到输入信号ur,作为纠偏电压ue,以保证线圈组件保持在所需要的正确位置。电磁力的大小和方向,取决于线圈中控制电流i的大小和方向。通过改变输入电压信号的方向,来改变电磁力Fcd的方向,从而实现双向运动。这样,系统由闭环控制,也提高了其控制精度和响应速度。
电磁力Fcd总是正比于电枢电流i,而感应电动势E总是正比于动子速度vc,比例系数分别称之为电磁力常数和反电动势常数,两者的取值略有差异。电枢反应的影响,但大体相同,近似为气隙磁感应强度Bg与有效绕组长度la的乘积。另外其在行程范围内无需换向,线圈电感在行程范围内基本不变,因此该动圈式直线电机具有良好的可控性。
组合线圈设计
线圈是动圈式直线电机的关键元件,其主要作用是把电能转换成机械能,广泛应用于执行机构的控制等领域。目前常用的线圈绕线方式为单线圈组合方式,其响应速度及电磁力有限,转换效率低,难以满足现节能环保和高效快速的要求。文中将原线圈平均分为多段,将其并联使用。不仅大大减少了线圈的重量和能耗,降低了材能的损耗,而且能满足大电磁力和高频响应性的要求。
相同电压下,单组动圈线圈串联组件电路可以减少响应时间,提高响应速度,但难以实现装置的大电磁力输出。只有保持电路中线圈组在磁场中作用线圈的长度才能保证装置的大电磁力输出,可以通过并联线圈组的方式来增加电路中通电线圈的长度来增大电磁力,相对于单组线圈的反电动势不增加。采用动圈式线圈均匀分割并联可以减少装置的电阻、电感,减少电阻、放大电流,大大地提高了装置的电磁力输出;但由于其电感相对太小,对动圈式直线电机的响应影响不大。
如果通过电流过大,产生的磁场与气隙磁场相互作用,造成磁场的非线性限制;长时间通以大电流,工作温升快导致发热损坏,电机工作时间和寿命受到一定限制;线圈电感的存在导致工作电流总是简便达到稳态。
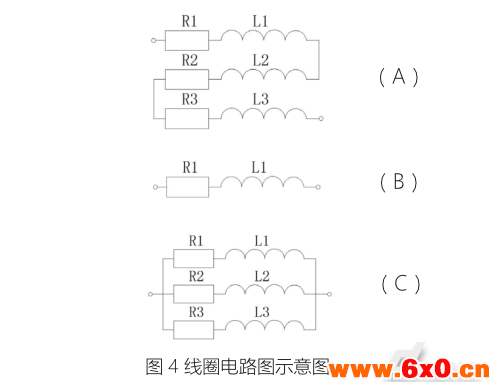
图4为三组线圈电路图示意图,假设如下:
(1)A组电路如图4(A)中,开关S1闭合,电感为LS1、电阻RS1。称为:串联的A组线圈;
(2)B组电路如图4(B)中,开关S1、S3闭合,电感为LS2、电阻RS2。称为:单组的B组线圈;
(3)C组电路如图4(C)中,开关S1、S2、S3闭合,电感为LS3、电阻RS3。称为:并联的C组线圈;
式中:电感量表示线圈本身固有特性,与电流大小无关,其表达式如下:

由于输入电压一定时,线圈的电阻、电感影响整个电路的时间常数和电流大小。在单线圈输入电流I不变的情况下,电磁铁的响应时间t:

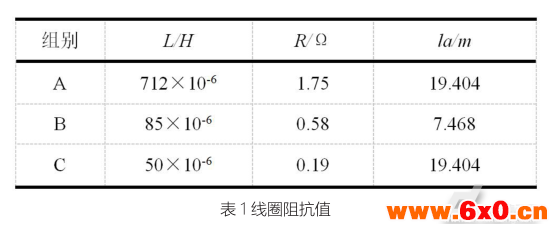
通过分析动圈尺寸和线圈阻抗之间的关系,可知线圈电感与电机线圈(绕线部分)长度、直径及线圈匝数的平方成正比,为了达到高响应在设计时必须降低线圈电感。采用图5所示DT-9935型LCR数字测量仪测得线圈组的电感L、电阻R如表1。

文中动圈式直线电机的独特之处是即通过对线圈的分割从而是工作线圈的工作时间和响应速度增加,再运用PWM控制方式组合线圈并联提高工作线圈的电磁力。针对载流线圈采用新型线圈分割再串、并联变换组合方式,采用PWM脉宽调制的控制对其线圈电流的大小及方向进行控制。
PWM控制回路中,线圈的循环工作主要是利用D触发器输入循环工作信号来控制线圈的运行,电流的大小主要采用脉宽调制的方式进行控制,即通过控制信号的占空比来达到控制电流大小的目的,进而改变改变电磁力的大小。同时,控制信号与控制脉冲振荡信号通过门电路对对应两个驱动三极管交替导通和截止,控制三极管输出脚向外输出相位差180°的脉宽调制脉冲,满足整个装置对频率的需求,如图6所示。
本文中为保持电机尺寸参数一定,能够通过分割长线圈改变为短线圈组,以改变线圈的匝数调整线圈电感值和电气时间常数。
建模与仿真
在工作气隙内,根据文献载流控制线圈(动圈)在均匀磁场中的受力公式,可得电机的可动线圈组件空载力特性,如下:
式中,Ki-动圈式电-机转换器的电流-力增益(N/A);i-线圈电流(A);Bg-气隙磁感应强度(T);la-线圈有效绕组长度(m)。
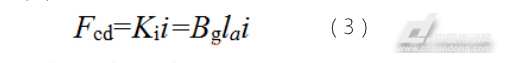
线圈端电压动态方程为:(4)
式中,u-线圈端电压(V);Ku-放大器增益;ui-信号电压(V);Rc-线圈电阻(Ω);rp-放大器内阻(Ω);L-线圈电感(H);Ke-线圈速度感应反电动势常数;E—感应电动势(V);vc—动子速度(m/s);xc-线圈组件位移(m)。
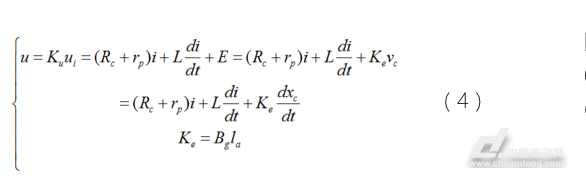
在线圈组电路两端稳定输入,线圈组件动态方程为:
式中,Mc-线圈组件的质量(kg);Bc-线圈组件的粘性阻尼系数(N·s/m);Kc-线圈组件弹性阻尼系数(N/m)。
综合公式(3)、(4)及(5)得到输入电压ur与位移xc的
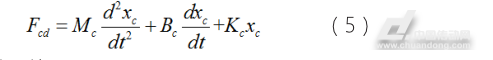
三阶传递函数:
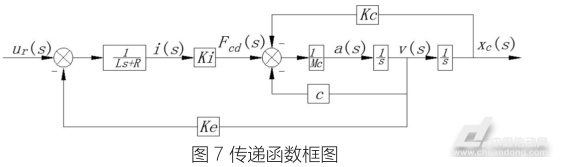
对上述的电机的动力学方程组进行拉普拉斯变换,可以给出以信号电压ur为输入量,以线圈组组件速度vc为输出量的动圈式直线电机传递函数方框图,如图7。
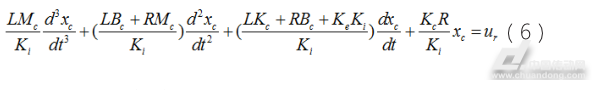
位移阶跃响应分析
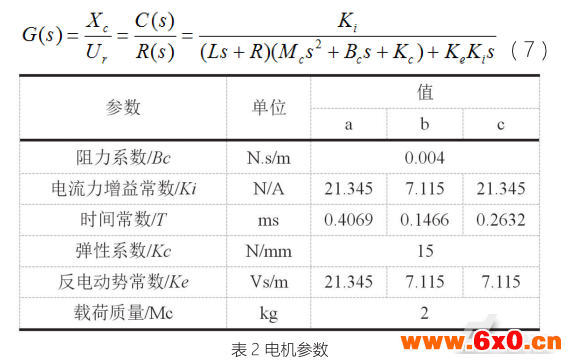
对图7所示传递函数框图,可得电机的数学模型,如下:
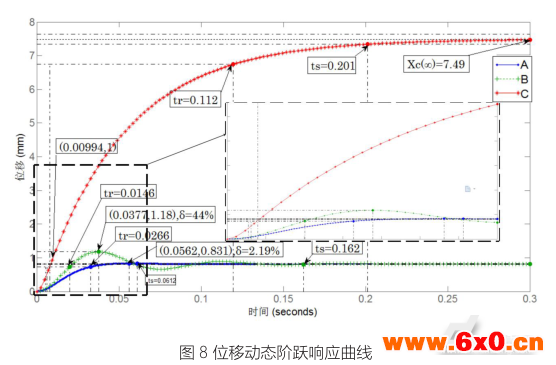
对上式(7),采用表2所示的参数,通过MATLAB仿真分析后,得到电机位移动态阶跃响应曲线,如图8所示。
从图8可以看出,对于单位阶跃信号输入,A组线
真分析后,得到电机位移动态阶跃响应曲线,如图8所示。
从图8可以看出,对于单位阶跃信号输入,A组线圈和B组线圈的位移幅值变化比较小,最终幅值稳定为0.8mm,其上升时间tr分别为26.6ms、14.6ms;并联的C组线圈的幅值变化比较大,最终幅值稳定为7.5mm,其上升时间tr为0.112s;在单位信号控制下,C组线圈的位移Xc=1mm时,tXc=9.94ms。由此可见,在单位信号控制下,可以采用并联线圈的方式使得改善其位移特性,其响应时间可减少到9.94ms。
结论
在相同电压工况下,与动圈组件串联相比,单组动圈线圈组件电路电阻小,电感小,可以减少响应时间,提高响应速度,但难以实现装置的大电磁力输出。只有保持电路中线圈组在磁场中作用线圈的长度才能保证装置的大电磁力,通过并联线圈组的方式来增加电路中通电线圈的长度来增大电磁力,相对于单组线圈的反电动势不增加。本文验证了均匀分割的线圈组件通过并联设计,其位移的阶跃响应达到1mm左右的时间由大于14.6ms减小到9.94ms以内,响应速度增加了1倍以上;其电磁力由原来的10.8N增加到93.2N,加速度也扩大了8倍。结合PWM控制方式可实现更高频响应的控制,电磁力达到最值的响应时间减少到0.688ms,大大地提高了整个装置的高频响应特性,实现了输出位移响应时间短、电磁力大等特点。该动圈式直线电机可广泛应用于电机直驱型数控一代产品等各类需要高响应速度的自动控制系统,前景良好。
文/广州中国科学院先进技术研究所、广东工业大学机电工程学院、深圳先进技术研究院罗良维 张弓 梁济民 王卫军徐征 顾星 郭云鹏 梁松松











 QQ交流群
QQ交流群

