摘要:文章为镜头驱动的小型直驱系统设计了具有低速大转矩特性的轴向永磁游标电机拓扑结构,该结构采用环形永磁体和集中式绕组,使其适应有限的电机安装空间和转矩输出要求。设计中采用永磁电机的磁路解析模型和有限元分析法评估对比了电机的主要稳态特性,验证所提出电机在0-100rpm低转速下的运行特点,为该类型电机的设计提供依据和经验。
1引言
在镜头驱动系统中,根据驱动电机的安装位置不同通常分为以下几类:机身驱动型、镜头驱动型以及机身镜头双驱动型。其中镜头驱动型(驱动电机直接安装在镜头中的类型)使系统减少了减速器和柔性联动机构设置,其电机性能一般比机身驱动电机优越,但要求使用能实现低速高转矩的直驱电机。目前,大多数的直驱应用场合是通过减速装置实现低速大转矩驱动的,传统的精密变速装置虽然技术相对成熟,但通常体积较大、噪声较大、效率较低,因此无需变速装置的低速大转矩直驱电机是迫切需要的[1]-[3]。将直驱电机应用于小型镜头驱动系统中,可以直接进行电磁能和机械能转换,减小能量损耗;同时,传统电磁电机又可以借鉴成熟的电机控制策略,与借助于压电陶瓷的超声波电机[4]驱动器对比,实现电机的精密稳定控制。
永磁游标电机是一种热门的轴向磁场型永磁同步直驱电机,因其多极设计具有低速高转矩的“磁性齿轮”特性[5]-[6],克服了传统永磁同步电机在直驱应用中的诸多不足,具有较好的应用和研究前景。游标电机机理较传统永磁电机复杂,但独特的设计原理使其不依靠减速齿轮便具有低速高转矩特性,因此在直驱系统中应用较广。尽管永磁游标电机在转矩密度方面,较磁齿轮复合电机性能尚有落后,但永磁体用量减小了接近一半,而较传统永磁电机而言,转矩密度有了大幅提高。同时,合理的极数设计和齿槽优化可使游标电机的大转矩特性发挥到最优,且同等功率等级的盘式轴向气隙磁场设计相较径向磁场设计可进一步减小电机体积,提升转矩密度[7]。
因此,本文立足于小型镜头驱动系统应用,参考现有的环形超声波电机安装方式,提出了采用轴向永磁游标电机结构的设计方案,通过磁路解析法和三维有限元仿真法对电机在低速区的稳态特性进行评估,探索总结低速大转矩电磁电机在此类工况下的运行特点和优化方案。
2电机设计与分析
2.1轴向永磁电机结构
所提出轴向永磁游标电机(如图1)具有平行的定转子结构和轴向气隙磁场,其主要优点为体积小、重量轻、调速性能好和可靠性高等,符合高负载镜头对驱动电机的安装体积限制和高转矩输出要求。电机单层气隙设计为0.3-0.5mm,主体结构为定子和转子,定子包含定子铁心和绕组,转子包含转子铁心和环形永磁体。为减小磁路中的涡流损耗提高电机效率,铁心一般采用冷轧硅钢片。径向电机的硅钢片可直接冲压而成,而轴向电机在铁心中具有轴向磁路,不能直接采用压制硅钢片,而是通常将卷起的硅钢薄层轴向切割出所需齿槽结构。同时,采用环形结构永磁体设计可以有效减小漏磁,提高气隙磁场强度和磁路的利用率,同时损耗的降低可以提高电机效率。
表1列出了电机运行过程中主要参数要求,由电池供电,平均转矩输出要高于200gf.cm,同时调焦过程中的振动和噪声不能过大,量化为额定50rpm转速时的噪声低于40dB。

2.2等效磁路解析法
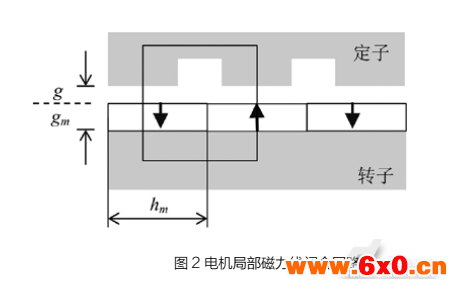
为清楚描述各参数间关系,图2展示了所提出轴向电机的横截面示意图,给出了部分电机参数定义。同时为了便于分析,作如下基本假设:
1)定、转子铁心的磁导率无穷大;
2)永磁体相对磁导率取其实际磁导率,且永磁体极间空气区域的相对磁导率与永磁体相同;
3)分析区域在二维平面内,不计端部效应;
4)定子槽为径向开口槽,槽内每个线圈边的电流密度均匀分布。
为求解空载气隙磁场的磁动势分布,根据安培环路定律,忽略定转子铁心的磁动势,则根据图2中磁力线回路得到

其中,Fg为气隙磁动势,Fmag为永磁体磁动势,Br为永磁体剩磁,gm为永磁体轴向厚度,μm为永磁体磁导率,g为气隙实际长度。上述磁动势为各自的基波幅值,充分考虑气隙磁场不同位置的磁密分布,可将气隙磁动势的表达扩展为
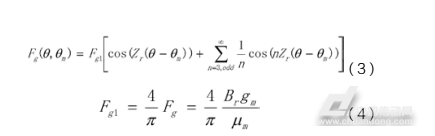
其中,Fg1为基波幅值,θm代表以定子为参照的转子位置角,θ代表定子上某一位置与参照轴之间的机械角度,Zr为永磁体极对数,n代表气隙磁动势谐波次数。在表贴式永磁电机中,计算气隙等效磁导可以简化为计算单位面积下的气隙磁导,将齿槽结构近似为图3,其中气隙磁导分为两部分P0(无槽表面到转子之间)和P1(开槽到转子之间)计算。单位面积上的气隙等效磁导推导如下
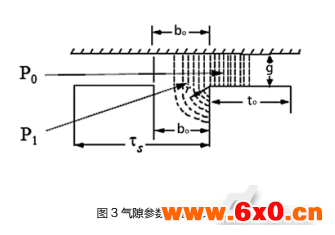
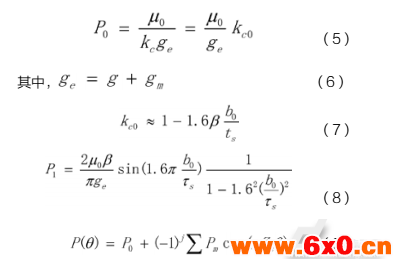
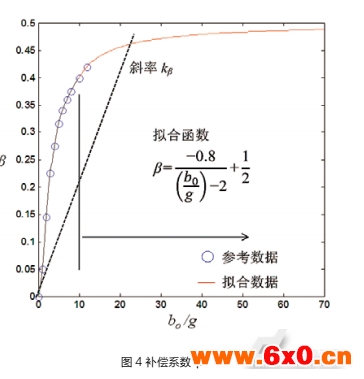
其中P0为定子无槽表面到转子的气隙磁导,P1为定子开槽到转子气隙磁导,Pm为气隙磁导的m次谐波分量,μ0为真空磁导率,b0为槽口宽度,ts为齿距,m为谐波次数,Zs为定子槽数,j为偏离短距绕组的槽数(整距绕组中j=0)。ge为气隙等效长度,因永磁体磁导与空间接近且表贴式安装,故计算磁导时永磁体可按空气对待。β被定义为一补偿系数[8],其中β与槽宽/气隙长度的比有如图4关系:
气隙磁场强度BPM=P(θ)F(θ),进而得到反电动势e(t)和电磁转矩T(r)的表达式为
其中,λ为每相磁链,N为线圈匝数,Dg为气隙平均直径,l为气隙的径向长度,ω为机械角速度,α为定子齿距对应的角度,kT为电机转矩系数,Irms为绕组线电流有效值,Ri为气隙内径,Ro为气隙外径,r代表气隙某一位置处半径。此外,为有效提高电机运行的平稳性,该结构下的齿槽转矩需要最大程度上减小,探讨影响齿槽转矩大小的电机设计参数关系。根据上述磁场参数的解析关系,齿槽转矩可由解析法表达为
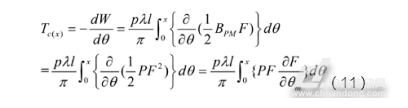
其中W为空载时永磁体产生磁场在主气隙中的能量表达。
2.3三维有限元仿真与对比
电机运行中同时存在永磁体磁场和电枢电流产生磁场,图5即为电枢通电后的磁场强度分布图,其中最大磁场强度在1.7T附近,铁心不存在饱和风险,可允许一定的过载运行,符合电机设计要求。
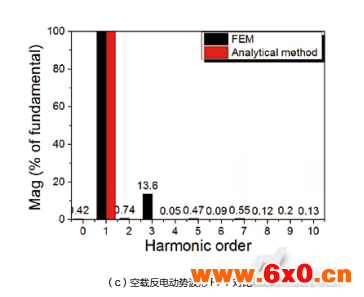
图6将通过磁路解析法和三维有限元仿真法得到的轴向永磁游标电机工作在50rpm时的稳态特性进行对比和分析,依次为电机的电磁转矩曲线、空载反电动势曲线及其谐波分析、齿槽转矩曲线及其谐波分析。其中等效磁路法在空间维度上的电机和材料参数为定值,因此数值关系计算出的电磁转矩为恒值,如图6(a)。同时等效磁路法无法设置铁心材料BH曲线特性及无穷的谐波次数,因此未能反映磁路饱和特性,所得反电动势波形较有限元法更加理想正弦化,如图6(b)。
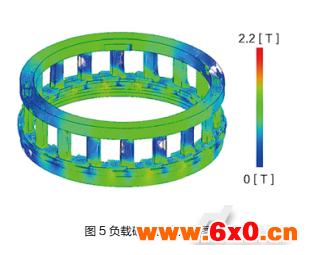
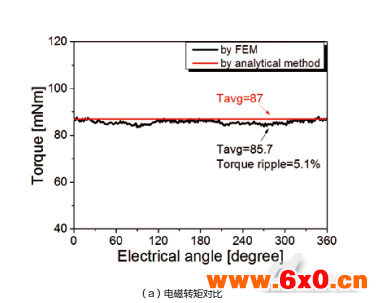
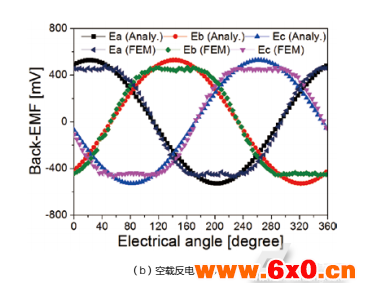

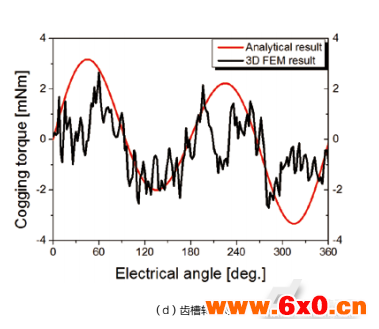
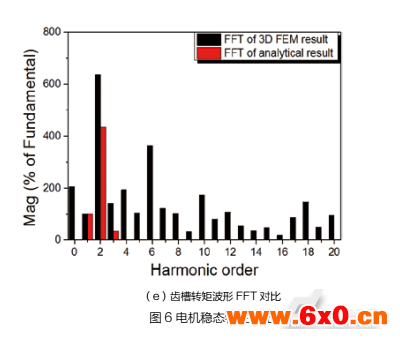
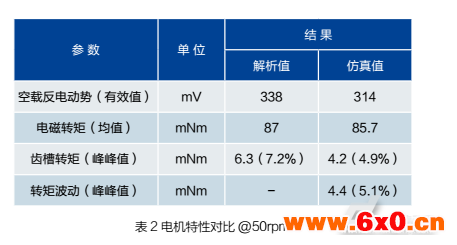
表2总结了磁路解析法和三维有限元分析法所得电机稳态性能对比,由于磁饱和效应的产生两者空载反电动势有效值相差7.6%,电磁转矩平均值相差1.5%,两组结果中齿槽转矩峰峰值都低于平均电磁转矩的7.5%,说明了磁路解析法对电机性能的评估偏差不大,可通过更多补偿系数的设置提升精确度。
3结论
本文立足小型直驱系统应用,设计了一款符合镜头安装要求的轴向永磁游标电机,并从磁场分布、反电动势、齿槽转矩、电磁转矩、转矩波动等方面对该电机进行了有限元计算分析,并与解析建模结果进行对比,说明了电机稳态特性并验证磁路解析模型的可靠性,为该类型电机的设计提供依据和经验。










 QQ交流群
QQ交流群

