温升是电机的关键、重要的性能指标,在实际的设计和计算过程中,往往会出现设计值与试验值的偏差问题,分析原因基本有两种,一种是制造过程对设计的偏离导致实际数据与理论数据的差异性,另一种原因是设计计算过程的不合理性。小编今天与大家介绍一下牛顿散热定律和散热系数在电机温升计算过程的应用。
牛顿散热定律和散热系数
实际上计算由对流作用带走的热量时,为了方便,都采用牛顿散热定律,具体见式(1)。
q=α(θ1-θ2)=αθ………………(1)
式(1)中:
q——热流强度,单位:瓦/米2;
α——散热系数,单位:瓦/米2﹒℃,即当表面与周围介质的温差为1℃时,在单位时间内由单位表面散发到周围介质的热量;
θ1、θ2——分别为固体和流体的温度。
利用式(1),在α为已知的情况下,只要知道q,就可求出温差θ,或者相反。这种计算方法之所以简单,是因为采用了散热系数。而把许多计算上的困难回避了。
但是决定表面散热能力的因素很多、很复杂,要十分精确地确定散热系数α也是很困难的。一般情况下,α值只能用实验来确定,且所得的α值,只能用于条件相同或类似的情况,否则计算结果的可靠性或准确性将大大降低。
用空气作为冷却介质时,其物理性能比较稳定。若忽略散热表面几何尺寸等因素的影响,则可近似近地认为电机各部件的散热系教仅与空气的流速有关。根据实验,当空气流速在5~25米/秒的范围内时,α与ν之间的关系可按式(2)表示。
α=α0(1+k0ν)………………(2)
或较准确地表示为式(3):
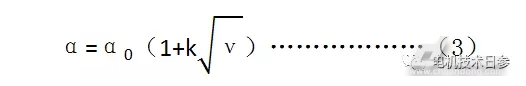
式(2)和(3)中:
α0——发热表面在平静空气中的散热系数;
ν——空气吹拂表面的速度;
k0、k——考虑气流吹拂效率的系数。
不同特征下相关系数的取值原则
发热表面在平静空气中的散热系数与表面的特征有关:涂以油灰和漆的生铁或钢的表面(如电机的机座和轴承外壳)α0为14.2;未涂油灰但已涂漆膜的生铁或钢的表面,α0为16.7;涂以无光漆或光漆的铜的表面,α0为13.3。
如果速度v用米/秒表示,则电机旋转时,转子外表面的k0=0.1,电机定子绕组端部的k0=0.05~0.07。系数k可按以下规则选用:
最完善吹风的表面,k=1.3;
电枢端部的表面,k=1.0;
电枢有效长度有表面,k=0.8;
励磁线圈表面,k=0.8;
换向器表面,k=0.6;
机座外表面(牵引电动机),k=0.5。

现实生活中,不少的电机厂家采用现成电机计算程序,而对于程度本身的内涵不是很清楚,Ms.参建议,我们有必要通过必要的手段,对程序的完善程度、合理程度进行分析,当然,没有足够的专业知识,该问题不太好解决,同样,对于程度的设计者,应通过理论的推导与现实的验证,使程序日趋完善。










 QQ交流群
QQ交流群

