改进BP算法在旋转机械故障诊断中的应用

针对BP算法在神经网络诊断中表现出来的学习收敛速度慢、易于陷入局部最小点等局限性，用改进BP算法——有弹回的BP算法，对转子试验台模拟几种常见的故障进行诊断研究，从中得出结论：将代表故障的信息输入训练好的神经网络后，由输出的结果，便可以判断发生故障的类型。此外，有弹回的BP算法大大地提高了网络收数速度和稳定性，更能满足实时在线诊断的要求。        人工神经网络的模型很多，误差反向传播算法BP网络是目前应用最广泛的网络模型之一，典型的BP网络是三层、前馈阶层网络，即：输入层、隐含层（也称中间层）和输出层。BP算法的基本思想是：输入信息的正向传播和误差的反相传播。在正向传播中，对于一个训练样本，将其特征向量输入神经网络，经过神经网络的前向传播计算，得到一个实际输出，然后将该输出与期望的样本输出相比较，若有偏差，则转入反向传播过程，将该偏差由原来的联络通路返回，通过调整各层神经元的联系权值，使误差减小；然后，再转入正向传播过程，反复迭代，直到误差小于等于允许值。，学习才结束。因此，学习训练包括输入向量的前向传播和误差的反向传播两个过程，可见三层前馈网络的优点就是具有很强的非线性映射能力和柔性的网络结构，但是因为BP网络采用了按误差函数梯度下降的方向进行收敛的，这就不可避免地出现了网络学习收敛速度慢，以及容易陷入局部极小点的问题^[1]，针对以上缺陷，应用改进BP算法对转子试验台的几种常见的典型故障进行诊断研究。        一、改进BP算法        为了改进BP神经网络的缺陷，人们曾提出了很多改进方案，常见的有自适应修改学习率算法、有弹回的BP算法、共扼梯度算法等，本文采用有弹回的BP算法来改进网络的收敛速度。三层及其以上的BP神经网络，常常使用传递函数如下：

        以下简称为S型函数，S型函数的特点是可以把无限的输入映射到有限的输出，而且当输入很大或很小的时候，函数的斜率接近于0。这使得在训练具有S型神经元的三层及其以上的BP网络时，计算出的梯度g_（k）会出现很小的情况，这时网络权值和阀值的改变量也会很小，从而影响了网络的训练速度。        有弹回的BP算法的目的就是为了解决这个问题，以消除g_（k）值对网络训练带来的影响。在该算法中，g_（k）的符号决定了网络权值和阀值的变化方向，通过预先设定的参数ξ来更新网络的权值和阀值。当网络性能函数对某权值的微分在连续两个训练周期内具有相同的符号时，权值的改变量将通过ξ得到增加，反之就通过g减小。如果该导数为0，那么权值改变量保持不变^[2]。        二、转子试验台模拟故障诊断的BP网络建立        1．转子试验台的建立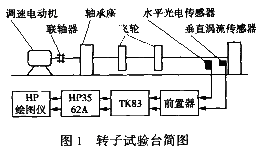

        如图1所示为一个故障模拟转子试验台，振动信号经水平光电传感器和垂直涡流传感器传至前置器及各分析仪，试验台转速可调。        2．网络的输入输出向量的选择及结构的确定        在模拟故障诊断的过程中，取振动信号的频域特征作为故障征兆，选取：(0~0.25)X、(0.25~0.75)X、 (0.75~1)X、1X、2X、3X、高次偶频、高次奇频等8种具有代表性的频率成分作为特征频率，其对应的谱值作为故障征兆，在如图1所示的转子试验台上模拟如下故障原因：转子质量偏心、局部碰摩、全周碰摩、不对中、转子裂纹、联轴器故障、油膜振荡、支承松动^[3]。以故障征兆Ak=（a₁， a₂，…，a₈）为网络输入，故障原因Y_k＝（y₁，y₂…y₈）为网络输出进行训练，相应的故障目标输出1代表有此故障，输出0代表无此故障^[4]。        神经网络输入层、输出层的神经元个数可以根据研究对象的输入、输出信息来确定，一般情况下隐含神经元数目n_H。可按下式给出^[5]：n_H= 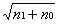+l，式中n_H为隐含层神经元数目，n₁为输入层神经元数目，n₀为输出层神经元数目，l为1~10之间的整数。在本试验中，n₁=8，n₀=8，n_H =5。        3．振动信号的归一化处理        分别取振动信号频谱图中的（0~0.25）X、（0.25~0.75）X、（0.75~1）X、1X、2X、3X、高次偶频、高次奇频分量作为特征值。在其进入网络训练之前要进行数据的归一化处理，即，令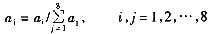

        这样，网络所有输入都在[0，1]之间。        4．神经网络训练       

        表1列出了试验过程中在（0~0.25）X、（0.25~0.75）X、（0.75~1）X、1X、2X、3X、高次偶频、高次奇频等8个频段实测的幅值经过归一化处理后的当量值，作为每个样本的故障特征值和试验过程中模拟的典型故障样本的目标输出。可见本试验的输入样本的值都很小，所以有弹回的BP算法很适合。        5．网络的训练结果        在本试验中，取网络的总误差允许值ε= 0.00001，α_k =0.5，将试验所获得故障征兆A_k 输入网络，经过约370次的训练后得到如表2所示的网络的实际输出。

        当诊断对象发生具体故障时，根据网络输出层节点的实际输出的数值来做出判断。例如，当第1个故障样本的8个故障特征值输入给网络输入层节点后，则得到网络输出层节点与其对应的实际输出为表2中的第1故障样本的8个输出值，其中只有y₁= 0.9993，接近1，而其它输出均远小于0.9993，可以近似为0，所以改进BP神经网络故障诊断的结论为“故障1”（转子质量偏心）发生，其它类型的故障以此类推即可得出。        此外，本试验还把改进后的BP算法的输出与普通BP算法的输出进行了比较，采用普通BP算法得经过8861次的训练才能得到如表3所示的网络的实际输出。  

      三、结论        由表2与表3的结果比较可知，采用有弹回的BP算法对设备的故障进行诊断和预测，比采用普通BP算法大大的提高网络的收敛速度，同时本试验还对这两种算法网络的收敛曲线进行了比较，得知：普通的BP网络有时很不稳定，在规定的训练次数内无法达到预期的要求，而且当训练进入平坦区时网络收敛速度就更加缓慢，有时甚至不收敛，而改进后的网络稳定性很好，能很快的通过平坦区，更能够满足实时在线诊断的要求，此外，利用改进BP算法神经网络提供的理论方法和技术手段，为建立智能化的系统状态监控和故障诊断提供了强有力的方法，具有广泛的应用价值。