
图1 stribeck曲线
D.Dowson基于线接触弹流润滑计算结果,提出了图2所示的润滑状态图。按膜厚由薄到厚依次划分为边界润滑、混合、弹流和流体动力润滑四个区域,并认为流体膜薄至表面粗糙峰顶出现边界膜时即开始进入混合润滑,还进一步提出25mm为弹流润滑向混合润滑转变的膜厚值。
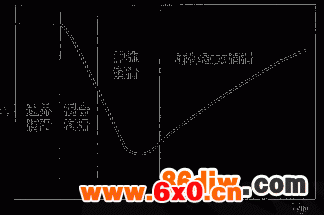
图2 润滑状态图
1989-1991年H.A.Spikes等通过对纳米级润滑膜的研究,提出了超薄膜润滑的概念(Ultra-thin film lubrication),1992年Leeds-lyon会议上重点讨论了薄膜润滑,近十多年来围绕弹流润滑向薄膜润滑转化进行了大量工作: 1.从弹流润滑向薄膜润滑转化的条件主要取决于润滑膜厚度,当弹流膜厚减薄到一定数值时,膜厚变化规律偏离弹流润滑理论,即膜厚—速度J载荷在对数坐标图上不再呈线性关系。至于转化膜厚除Dowson提出的25nm外,Johnston等通过实验发现转化膜厚为15nm。Streator和GerhardsteinH实验表明值为23nm。雒建斌实验得出弹流理论适用的最小膜厚极限值,当分别采用13604号基础油、液体石蜡和10号矿物油为润滑剂时和配副材料分别采用GCr15、表面镀Cr和Al与玻璃盘时,不同润滑剂的最小膜厚的极限值分别为15nm、20nm和24nm,不同配副材料的最小膜厚:当速度高时分别为27nm、25nm和18nm;当速度低时分别为19nm、18nm和12nm,即上述极限值随润滑剂、配副材料(表面自由能)和运行条件而异。 2.根据摩擦副表面吸附膜、有序液体膜和无序的流体效应膜厚度的变化关系区分润滑状态的转化,以流体效应为主导的润滑状态为弹流润滑,以有序液体膜为主导时的润滑状态为薄膜润滑,只有吸附膜的润滑状态为边界润滑。 3.根据膜厚和膜厚比划分润滑状态,如表1所示。
表1 润滑状态的划分

4.根据油膜厚度与表面综合粗糙度和润滑剂分子的有效半径Rg之比划分润滑状态(图3)。

图3 润滑状态图
由上可见薄膜润滑不同于其他润滑状态,主要在于其尺度处于纳米量级。 二、薄膜润滑研究 1.理论基础 流体润滑(包括弹流润滑)的理论基础是粘性流体动力学,薄膜润滑是从原子和分子结构出发,研究纳米尺度下的表面和界面分子层的摩擦学行为,其理论基础主要是表面物理学和表面化学。 2.物理模型 Israelachvili等认为薄膜润滑的复杂摩擦学特性是由于薄膜结构相互转化,提出了不同的摩擦条件,壁面分子排列呈现固态(Solid)、无定形(Amorphous)态和液态(liquid)。 Smeeth等认为对含高分子的合成油在固体表面附近形成一层富集的高粘度的高分子吸附膜,提出了体相粘度的弹流润滑状态向基于高分子粘度的弹流润滑状态转化的物理模型。此模型的局限性在于没有考虑到润滑油分子在固体表面附近形成静态吸附膜和极薄油膜的物理性能随时间的变化。 Miyamoto等认为表面力直接作用于表面,在液—固表面间的表面力有:静电力、范德华和溶解力,其中静电力与表面电荷交换有关,范德华力和溶解力与液体动压力耦合。当两固体表面间隙>5nm时表面力可以忽略不计。当间隙为1nm时,表面力产生的当量压力与粘性压力同数量级。提出了考虑表面作用的模型。 雒建斌认为在薄膜润滑状态下,油膜除了吸附膜和流体膜外,还存在兼有流体膜和吸附膜二者性质的有序液体膜。提出了薄膜润滑动态物理模型,即有序液体模型(图4)。

图4 薄膜润滑模型
沈明武采用平均为5nm的超细金刚石粉(UDP)作为添加剂,加入不同的基础油中,发现在该润滑状态下,分散在润滑油中的球形纳米颗粒对摩擦副表面产生犁削作用形成微滚道,随后在微滚道中产生滚动效应,提出含固体颗粒的薄膜润滑模型。 3.分子动力学模拟 当润滑膜厚度接近分子和原子量级时,连续介质力学的假设不再有效,从统计物理化学中形成的分子动力学模拟(Molecular dynamic simulation)方法被成功地用于薄膜润滑性能的计算、分析。它把连续介质视为n个原子或分子组成的粒子系统,通过数值求解运动方程得到所有粒子的运动规律,再由统计平均得到该系统作为连续介质的宏观性质。此法根据模拟研究对象的不同从统计物理角度可分为平衡态分子动力学模拟和非平衡态分子动力学模拟。除上述模拟方法外还有MC(Monte Carlo)法,它用于解积分方程的随机过程,把粒子的运动用随机方法模拟,运用统计力学的基本观点统计出平均结果等。目前用得较多的是分子动力学模拟。 Harrison等对单原子分子流动、Magda对液Ar在2-12层分子厚的平衡特性、Heinbuch等对平面Poisuille流、Schoen等对5个原子厚的薄膜剪切流、Thompson等采用面立方晶格壁对剪切流、胡元中等采用简单的球形分子模型对压力流和剪切流,以及采用珠簧模型对癸烷和十六烷的剪切流等进行了分子动力学模拟,揭示了液体润滑剂在纳米薄膜中的性质变化。如:当润滑膜厚度减小至纳米尺度时,液体的等效粘度随着膜厚减小而迅速增大,即表明液体在固体壁面约束作用下逐渐失去其流动性而向固态转化。当在固定膜厚下增加系统压力至一定值时,发现液体的粘度和密度均有阶跃现象,表明有固化相发生,又上述转变压力低并随膜厚的减小而下降,因此薄膜中间润滑剂常处于固态或类固态状态。 在平行壁面的平面内,对粒子“显现概率”的统计表明,薄膜中液体分子存在一种与壁面结构相似的有序分布,其有序度随与壁面距离增加而逐渐消失,其实质是一种由壁面诱导的外延性有序结构。 通过对薄膜中粒子速度沿膜厚的速度分布曲线分析,发现在壁面附近和膜的内部有不连续突变,即出现“界面滑移”和“层间滑移”现象。其滑移率反映了薄膜中润滑剂的固化程度等。 上述模拟结果,验证了有关物理模型和实验结果,同时可看到上述分子动力学模拟的模型已从半无限的无结构壁到有结构壁,从硬球函数到L-J势到更复杂的势函数,从单原子到长链分子日益接近工程实际,取得了长足发展。至于方程数值解法传统的有限差分法已不适用,常用的有Euler.Gear.Verlet和Leap-frog算法等。 张朝辉基于连续流体理论进行了微极流体模拟、耦合应力与二相流分析和计及边界滑移润滑方程的求解,分别分析了薄膜润滑性能。指出:有序分子膜的存在其作用相当于增加润滑剂的粘度,因而增加了膜厚、提高了承载能力,且膜厚随载荷变化较平稳;增加固体颗粒浓度可使润滑剂的特征长度增加,从而改善其润滑性能;边界滑移将使压力波动、膜厚减小,降低承载能力等。 笔者等运用能量的观点分析了流体内部作用,提出由分子流代替微观粒子运动,使微观分析与宏观分析对接,得出了分子流的连续、动量和能量方程,应用相关函数理论表达润滑剂的性能参数;对计算中的关键粘度修正问题,由间隙内粘度变化的特点,提出了几种简化的实验粘度修正模型,并对实际轴承进行了性能分析,得出了一些薄膜润滑轴承性能的变化规律和薄膜润滑的实现条件,为将薄膜润滑推向工程实用作了初步尝试。 4.实验研究 Chan等利用表面力仪(SFA)进行挤压实验发现,当膜厚为8-10个分子直径大小时,Reynolds方程不再适用。Homola等利用SFA研究了低速稳态剪切下薄膜润滑的摩擦特性,综合考虑了压力、温度、壁面、速度、膜厚、不同分子等的影响,发现:a.在膜厚尺度接近分子量级时,润滑膜出现微“结构化”现象,并认为这是把液体视为无结构的宏观润滑理论失效的主要原因;b.对于壁面间呈短程排斥力的情况,即使载荷很大,也没有出现磨损破坏,摩擦力远比空气润滑时小;c.壁面间呈吸引力的情况,载荷很小时就出现磨损;d.对于壁面间作用力随间隙振荡性变化的情况下,光滑滑动出现在整数倍振荡周期的膜厚处e.超薄膜的行为特征在一些情况下更像固体而非液体。 Yamada等利用表面力仪对L-B膜的滑动摩擦进行了研究,发现静摩擦力与动摩擦力差值与滑动-静止-再滑动时的时间间隔有关。如果从静止到再滑动的时间间隔小于相变时间,由于膜来不及发生相变,所以静动摩擦力的差值为零;如果时间间隔大于相变时间,相变的发生导致了膜的特性变化,则动静摩擦力出现差值。 Granick等利用配有侧向测量机构的表面力仪,对薄膜的流变特性进行了研究,研究表明:a.等效粘度随膜厚的降低而明显上升,在薄膜状态下,其值的大小比体相(Bulk)状态时高几个数量级:b.随着膜厚进入分子量级,即使在体相状态下表现为典型牛顿流体的物质,处于薄膜状态时,在较低剪应变率下就会出现剪切稀化现象,因此,认为薄膜流体的松弛时间明显增大,可比体相状态高几个数量级;c.薄膜润滑状态下,流体呈现出弹性特征。还对临界剪应力和壁面间液体的“类固性”(Solide-like)进行了探讨,认为:a.壁面间液体转化为类固体不一定要较大的压力;b.类固态出现在室温,而不是由于温度达到凝固点。c.无论凝固时结晶与否的液体都出现类固态;d.临界剪切力随时间而增大,不是由于接触面积的增加而产生的,而是一种分子的重构。即认为类固态的出现是一种典型的膜厚效应。 邹鲲应用表面力仪,对十六烷的超薄膜特性进行了研究,发现:在超薄膜状态下,流体的等效粘度及弹性剪切模量随膜厚的减小而明显增大;十六烷在较低剪应变率下出现剪切稀化现象;随着膜厚从宏观厚度向超薄膜变化,十六烷从牛顿流体逐渐转化为粘弹体;有些润滑剂的膜厚随持续剪切时间的增加而增加,呈现剪切时间效应;不同膜厚下,摩擦力随剪切速度的变化呈非线性关系等。 Overney等用原子力显微镜(AFM)研究了硅表面LB膜的摩擦、磨损与滑动速度的关系,发现随滑动速度降低,摩擦力增加。Bhushan等用摩擦力显微镜(FFM)测试得了微摩擦力与表面轮廓斜率的对应关系。Mate等用FFM测得微摩擦力的周期性。Kaneko等用FFM测得微磨损的特性等。Scandella等用扫描力显微镜(SFM)研究了云母MoS2超薄膜的摩擦学性质。此外,Spiks,Streator和雒建斌等还运用改进的光干涉法实测了由弹流向薄膜润滑转变的膜厚值等。 三、小结与展望 1.纳米科技使人类在认识和改造自然方面进入一个新的层次,能进一步挖掘物质的潜力。它的发展无疑地将深刻影响国民经济和现代科学技术的未来。我们知道原子是组成自然界的基本单位,原子的排列方式不同,使自然界呈现多姿、多彩。从微观角度,如果说一个人有健康的身体,就说明这个人的肌体排列组成是合适的。如果能按自己的意愿排列原子的话,人类就可以对物质结构进行完全有效的控制,纳米科技的出现、深化和发展,则可能使上述设想成为现实。 2.纳米机械学的诞生是现代机械科学发展的必然结果,随着现代科技的进步,人们不断追求制造出尺度越来越小,而性能越来越完善的微型装置,特别是在生物、环境控制、医疗器械、航空航天、数字通讯、传感技术以及灵巧武器等领域。作为纳米机械学的重要分支纳米摩擦学(包括纳米薄膜润滑),日益为人们关注。 3.润滑状态不同,其形成机理、物理模型、流变性能、失效方式等均各异,因此要对润滑合理设计和维护,必须了解各运动副的润滑状态。薄膜润滑影响因素复杂,给设计、维护人员带来困难,同时亦带来契机,如可采用粘度低于或高于基础油的极性添加剂进行润滑性能控制,特别是目前各种纳米润滑油的研究成功和投入市场;又由于薄膜润滑状态下润滑性能与润滑剂分子的有序化程度有关,可通过改变外部环境如电场、磁场等对分子有序度进行控制以改善润滑性能。 4.实际运行工况复杂,在不同时刻有可能处于不同的润滑状态,因此要求在不同润滑状态下的润滑性能均处于最佳状态是困难的,这时需综合考虑各种润滑状态并突出重点,照顾一般。 5.有序分子膜提供了一种借助表面工程技术来控制润滑性能的途径,在前面介绍纳米材料科学中述及的各种有序分子膜,有的已付诸工程应用,取得显著成效。 6.薄膜润滑尚处于探索、研究阶段,关于润滑薄膜的构性关系(剪切摩擦力与分子排列方式、有序度强弱和润滑膜厚度之间的关系;各种参量对时间、膜厚和有序度的影响;润滑的失效机理及判断准则等)、薄膜润滑的数理模型和性能分析,膜厚、摩擦力、微观分子排列结构和有序度的测量等均有待进一步深化研究,特别是目前分子动力学模拟多采用简化分子模型和理想表面与实用润滑剂和工程实际均有较大差距。因此,要使模拟更接近实际工况,进而建立可采用一般连续介质力学方法进行薄膜润滑性能计算的薄膜流体的本构模型,形成统一的流体和薄膜润滑理论,日益为人们关注。又目前试验大多是采用纯物质或一些特殊的高分子材料进行研究,今后宜扩展至普遍润滑剂及添加剂,这样不仅使研究工作更接近实际,且为润滑油、添加剂等混合物的研究开辟了一个广阔的领域。










 QQ交流群
QQ交流群

