动力学分光光度法是利用反应速率与反应物,产物,催化剂浓度间的定量关系,通过测量吸光度对被测组分定量的一种方法。下面测定反应体系中催化浓度为例,介绍动力学分光光度法的基本原理及测定方法。
设一个在催化剂(F)的作用下进行的显色反应:

若D为有色化合物,则D的生成速率(显色反应速率)可表示为:
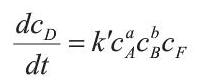
在反应进行的初期,A,B的浓度较大,反应小号的A和B可忽略不计,则可视为常数:
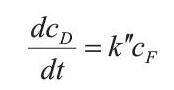
由CF变化也很小,可视为常数,上式积分得:
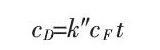
将上式代入朗伯比尔定率,有:
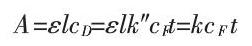
此式即为动力学分光光度法的基本关系式。
测定催化剂(F)的方法通常有固定时间法,固定浓度法和斜率法三种,固定时间发是让反应进行一固定时间后终止,然后测量反应体系的吸光度(A):
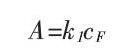
不同的催化剂浓度(cF)测得相应反应体系的A值,做出校准曲线,然后由加入试样的反应体系的A值求出试样中F的浓度。
固定浓度法是测量产物(D)达到一定浓度所需的时间,此时式中的CD为常数,则:
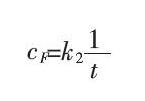
同样地可以作出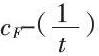 校准曲线,由试样体系的t值求出催化剂(F)的含量。
校准曲线,由试样体系的t值求出催化剂(F)的含量。
斜率法是根据吸收光度(A)随反应时间的变化速率来测定CFO根据关系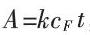 在不同的CD下测得A-t曲线,分别求出其斜率值。作出KCF-CF校准曲线。斜率法的校准曲线由更多的实验数据获得,因而其准确度较高。
在不同的CD下测得A-t曲线,分别求出其斜率值。作出KCF-CF校准曲线。斜率法的校准曲线由更多的实验数据获得,因而其准确度较高。
动力学分光度法具有灵敏度高,选择性好,应用范围较广等等特点,主要缺点是影响因素多,不宜严格控制,测定的误差较大。










 QQ交流群
QQ交流群

