1 引言
PID控制原理简单,适应性强,容易实现,是机器人控制的常用方法,PID控制系统设计的核心内容是如何确定其比例系数Kp、积分常数Ti和微分常数Td的最优解。控制参数的选定直接影响仿人机器人控制系统的响应速度、调节偏差的强度,以及控制系统的精度。
针对PID控制参数确定,主要有传统参数整定方法以及结合智能算法对参数进行优化。传统参数整定方法主要有试凑法、经验数据法和扩充临界比例度法。应用传统参数整定方法有时并不能达到有效的控制效果。近年来,随着智能算法的发展,模糊算法、神经网络以及遗传算法等都运用到PID参数优化当中。
其中遗传算法是一种新型的、模拟生物进化机制的随机化搜索和优化方法,具有并行计算、全局收敛、编码操作等特点。由于其算法结构的开放性,易于与问题结合,便于运算,已成功的应用于求解多种复杂的优化问题,遗传算法的特点使得将其运用于PID参数的优化是可行的。
针对仿人机器人PID控制参数优化存在的问题,结合智能算法的优势,本文提出了一种自适应遗传算法优化PID控制参数的方法,并在ADAMS环境下进行了仿真,得到较为满意的结果,表明该方法是可行且有效的。
2 仿人机器人关节PID控制
2.1 常规PID控制原理
PID作为最早实用化的控制调节方法,是模拟控制系统中技术最成熟的一种调节方式。PID调节根据给定值与实际值的偏差进行比例调节,并且引入积分、微分环节提高控制系统的性能和品质,其基本控制流程如图1。
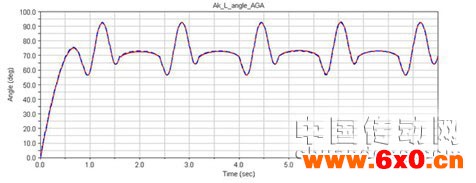
图1 PID控制过程示意图

在PID控制中,Kp、Ti和Td这3个参数的选择直接影响着PID控制的优劣,所以PID控制的设计关键问题始终是如何选择这三个参数。常规的PID控制器由于受到参数设定不良、性能欠佳以及对运行工况适应性较差的影响,往往达不到理想的控制效果,从而使PID控制的应用受到限制。
遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机化搜索方法,属于直接搜索法,对适应度函数基本无限制,既不要求函数连续,也不要求函数可微,因而采用遗传算法对PID参数进行调节是一种较好方法。但是,标准遗传算法在线性方面具有一些不足之处,而自适应遗传算法则是针对这些不足之处改进而来的。所以本文采用的是自适应遗传算法来优化PID参数。
2.2 基于自适应遗传算法PID参数优化
在仿人机器人行走仿真控制过程中,仅保证机器人行走过程的稳定性还不够,为了能够提高控制系统的响应速度与控制精度,必须寻找仿人机器人控制系统的最优PID控制参数以充分发挥控制系统的性能。基于遗传算法的PID控制系统框图,如图2。
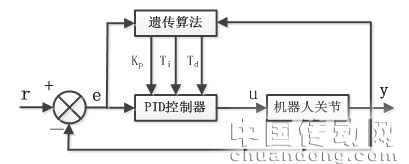
图2 遗传算法优化PID控制原理框图
2.2.1 自适应遗传算法
自适应遗传算法针对标准遗传算法进行如下改进:
1)根据适应度函数和进化代数自动调整个体的交叉率和变异率,AGA自适应交叉率、变异率按如下公式进行调整。
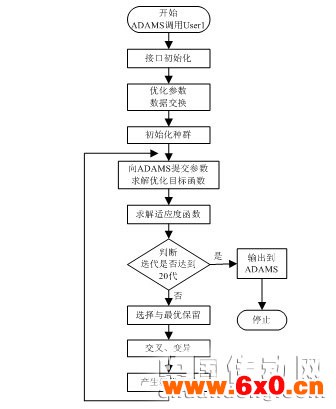

通过这种遗传算子的调整,当种群个体适应度较差时,赋予种群个体交叉算子的最大值和变异算子的最小值,保证算法能在进化过程中进行全局搜索;当个体适应度值较大时(个体优良),随迭代次数的增大,不断的减小交叉算子、增大变异算子,从而提高算法的局部搜索能力。
2)最优个体保留策略与新个体优良判别。通过对交叉、变异后产生的新个体进行适应度值的计算,并与原来个体的适应度值进行比较,能够有效选择更为优良的个体。
经过对标准遗产算法改进后的自适应遗传算法除了具有标准遗传算法的优点外,还具有如下优点:
1) 避免过早收敛问题,提高全局搜索能力;
2) 避免算法收敛时产生振荡,提高局部搜索能力;
3) 使遗传算子具有方向性,提高遗传算法的收敛性。
2.2.2 AGA程序设计
在AGA设计过程中,需要使用一系列算法参数,如选择、交叉、变异算子以及最大迭代次数等,在编写算法之前,先确定其相关参数。
1) 确定遗传算法的优化参数
在遗传算法设计中,算法基因与优化参数没有直接的联系,因此首先确定算法需要优化的参数:PID控制参数比例调节常数Kp、积分常数Ti和微分常数Td。通过选择最优控制参数保证仿人机器人的控制精度和响应速度。
2) 遗传算法编码
编码是将问题的解用一种代码方式表示,从而将问题的状态空间与遗传算法的解空间相对应。编码方式的不同不仅决定了染色体的形式,而且很大程度的影响遗传算子(选择算子、交叉算子、变异算子)的运算方式。编码方式对于不同的优化问题有所不同。主要的编码方式有:0-1编码、顺序编码、实数编码和整数编码。
本文为了保证优化的最优参数有足够的精度,采用实数编码的方式对PID控制参数进行编码,与之对应的染色体形式为:

3) 种群初始化
初始种群是遗传算法进行迭代优化的起点,其产生方式主要取决于编码方式,本文采用随机函数产生遗传算法的初始种群。
4) 种群规模ps
在遗传算法优化过程中,种群规模ps的确定对算法实现有重要影响。种群规模ps过小,则种群缺乏多样性,将导致进化的过早收敛,种群规模过大,则会导致计算收敛变慢,影响遗传算法的效率,此外种群规模对算法的选择压力和种群多样性等其他因素都有影响。因此合理的种群规模对算法十分重要,本文通过反复实验,最终确定种群规模为ps=20。
5) 适应度函数
在自适应遗传算法(AGA)中,适应度函数几乎是评价种群个体优良的唯一标准,群个体的选择复制、交叉、变异都与适应度函数密切相关。适应度函数通常有两种设计方法:第一种,原始适应度函数,也就是直接将目标函数作为个体的适应度函数;第二种,标准适应度函数,由于遗传算法求解过程中,适应度函数通常要求非负,且适应度函数越大,则种群个体越优良,通常目标函数需要做一定变换才能获得标准适应度函数。
本文中,仿人机器人控制系统主要控制仿人机器人关节力矩,通过力矩驱动仿人机器人关节运动,并保证仿人机器人实际输出的关节位移与理论关节位移相符合。因此本文中将仿人机器人行走过程中实际关节轨迹与理论关节轨迹的最大偏差作为控制的目标函数,目标函数越小,则控制精度越高,由于适应度函数要求适应度函数值越大,则个体越优良,因此,在这里需要对目标函数做一定的更改,将目标函数的最小值与适应度函数的最大值相对应,具体的办法是通过一个较大的数减去目标函数,获得适应度函数值,其函数关系关系式为:
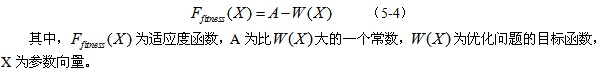
6) 遗传算子的确定
遗传算法的基本思想就是优胜劣汰,主要通过选择、交叉、变异方法,随进化代数的增加,最终获得最优个体。在进化过程中,选择算子、交叉和变异算子对算法性能产生很大的影响。
在遗传算法的设计中,不同的选择策略会导致不同的选择压力,选择压力过大,优秀个体复制较多,会导致算法收敛过快,最终导致早熟现象,压力过小,则种群多样化明显,会导致算法收敛过慢。常见的选择策略有:轮盘赌式选择、基于排名的选择和锦标赛选择。
本文中针对算法的适应度函数,采用适应度比例选择策略,如式5-3所示。同时对此方法做一定的修改,通过精英保留策略,在算法的后期,直接保留最优个体的基因,通过这种方法,可以有效避免在遗传算法的后期丢失最优个体的可能。

7) 终止条件确定
遗传算法的常见终止条件有两种,第一,实际值与期望值的偏差在公差允许的范围内时,算法迭代终止。第二,采用遗传算法的最大迭代次数作为算法的终止条件,并将最后一代种群中最优个体作为最优解输出。本文采用第二种算法终止方法,并规定最大迭代次数为20代。
3 仿真研究
3.1 遗传算法在ADAMS中的实现
根据上述自适应遗传算法对PID参数进行优化的基本思想,基于VC++语言编写AGA优化程序,通过ADAMS自带的控制工具箱,建立基于自适应遗传PID算法的控制系统,进行仿真,验证虚拟样机模型的正确性。
构建AGA结合ADAMS的仿真流程图。在优化设计过程中,ADAMS首先对接口进行初始化,将优化目标函数、设计变量与范围传递到遗传算法中,通过遗传算法产生初始群体,并将参数提交给ADAMS进行目标函数计算,遗传算法根据目标函数值计算个体适应度。然后判断终止条件,如果未达到终止条件,则通过遗传进化产生新种群,计算新的适应度值;如果满足终止条件,则向ADAMS提交最优解及相关参数,并终止优化程序。如图3。

图3 AGA在ADAMS中仿真流程图
其中将遗传算法引入ADAMS中,可以不用考虑遗传算法优化中机械系统的数学模型,就能很方便获得适应度函数值,简化了遗传算法的设计过程。
根据仿真流程图,以控制仿人机器人左膝关节轨迹为例,建立优化算法控制系统,进行仿真。
首先,建立优化设计的设计变量,即variable_P、variable_I、variable_D。由于遗传算法具有很强的全局寻优能力,因此确定variable_P的范围为[1,2500],variable_I的范围为[1,500],variable_D的范围为[1,2500],并将三个设计变量与控制系统PID环节关联以保证遗传算法的全局搜索。
其次,建立优化目标函数。以实际关节轨迹与理论关节轨迹差值的绝对值作为设计目标,目标函数值越小,控制精度越高。由于机器人关节轨迹为复杂的分段函数,为方便起见,采用样条拟合的方法将理论轨迹输入到ADAMS中。
最后,通过ADAMS的DesignevaluationTools确定优化目标与设计变量,并设置优化的相关属性,如显示设置、输出设置以及优化参数设置,将‘Optimizer…’中的优化算法设置为‘User1’,并进行仿真。
3.2 PID参数优化后处理
从优化结果来看,PID控制精度有明显的提高,AGA算法以最大迭代次数作为终止条件,收敛速度相对较慢但优化结果准确,说明遗传算法具有较强的全局寻优能力。
进入ADAMS/PostProcessor模块,可以将AGA优化仿真结果跟ADAMS软件自带的SQP优化模块仿真结果进行对比,图4的上半部分为AGA优化结果,下半部分为SQP优化结果,在两种算法中,控制偏差随时间的变化趋势大体相同,且偏差值大小相比为优化前都有大幅的减小,充分体现了优化设计在控制系统中的作用,如图4。
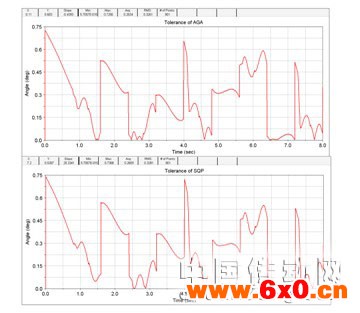
图4 优化目标函数值对比
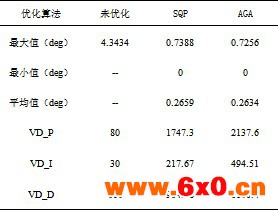
此外通过对目标函数进行数据处理,查看目标函数在控制过程中的最大值、最小值以及平均偏差值,可知使用遗传算法进行的控制优化,无论目标函数的最大值还是平均值,都比采用ADAMS自带的SQP算法的计算结果要小,见表1。
表1 目标函数各项数值对比
将AGA优化后的仿人机器人左膝关节角运动过程的实际轨迹跟理论轨迹重合情况跟优化前进行比较,图中,蓝色虚线表示关节角的实际轨迹,红色实线表示关节角的理论轨迹。仿真结果,如图5和图6。
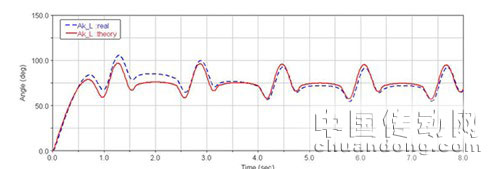
图5 优化前关节理论与实际轨迹重合情况

图6 优化后关节理论与实际轨迹重合情况
比较图6与图7中可以看出,控制系统经过自适应遗传算法优化后,其控制性能较之优化前有极大提升,关节运动的实际轨迹与理论轨迹更加接近,保证了仿人机器人行走的稳定性、可控制精度,提高了控制系统的实时响应速度,证明了基于遗传算法的PID控制系统参数优化方法的正确性。
4 结论
针对仿人机器人PID控制系统参数确定存在的问题,本文提出了基于自适应遗传算法定PID控制参数优化方法。将三个参数作为遗传算法的个体,采用仿人机器人的理论关节轨迹与实际关节轨迹的最大偏差值作为目标函数,适应度函数与之相对应,采用适应度比例选择策略,可以有效避免在遗传算法的后期丢失最优个体的可能,以保证机器人控制系统参数选择精度。通过ADAMS仿真结果对比分析,优化后的仿人机器人控制系统的控制精度、响应速度都有明显提高,说明了基于自适应遗传算法的PID控制能够得到比传统PID控制更优的结果。
参考文献
[1]金奇,邓志杰.PID控制原理及参数整定方法[J].重庆工学院学报,2011(7):91-94.
[2]于晓敏,于晓坤,耿蕊.PID控制器参数优化算法的仿真研究[J].计算机仿真,2008(5):212-215.
[3]姜玉春,吴红燕.PID控制器的参数整定[J].莱钢科技,2006(2):54-55.
[4]朱盈,朱俊.多种PID控制及其仿真比较[J].工业控制计算机,2010(1):53-54.
[5]牛芗洁,王玉洁,唐剑.基于遗传算法的PID控制器参数优化研究[J].计算机仿真,2010(11):180-182.
[6]WANGP,KWOKDP. OptimaldesignofPIDprocesscontrollersbasedongeneticalgorithms[J].ControlEngPrac,1994,2(4):641-648.
[7]杨智民,王旭,庄显义.遗传算法在自动控制领域中的应用综述[J].信息与控制,2000,29(4)14-17.
[8]张可村,李换琴.工程优化方法及其应用[M].西安:西安交通大学出版社,2007.
[9]黄友锐.智能优化算法及其应用[M].北京:国防工业出版社,2008.










 QQ交流群
QQ交流群

