1 引言
非线性系统在现实世界中普遍存在,可以说绝大多数系统是非线性的,例如卫星的定位与姿态控制系统、机器人控制系统、精密数控机床控制系统等等,这些都不可能采用线性模型,因此研究非线性系统的最优控制问题有重要的理论及应用价值。因为对非线性系统的最优控制,根据极大值原理会导致求解一个非线性的两点边界问题。一般来说,该类问题的解析解往往是不存在的,所以目前对该课题的研究主要集中在其近似解的求解方面,比如Galerkin逐次逼近法,求解非线性HJB方程的级数展开法,求解状态依赖的Riccati方程(Stata-DependentRiccatiEquation,SDRE)迭代解法,准线性化方法、梯度法等迭代方法,基于向量微分方程迭代的逐次逼近方法等等。近年来随着以微分几何为工具的精确线性化方法的发展,对部分非线性系统可以通过适当的非线性状态变换和反馈变换,实现非线性系统的伪线性化,从而应用成熟的线性系统理论和方法。
本文针对非线性单连接机器人系统给出一种设计精确反馈线性化最优控制器的方法。首先,给出非线性单连接机器人的系统模型,并对最优控制问题进行描述;其次,通过微分同胚坐标变换,将非线性单连接机器人系统模型转变为伪线性系统模型;再次,在此基础上给出了在关系度r等于系统阶数n的情况下基于二次型性能指标的最优控制器的设计方法;最后,通过求解Riccati方程得到系统最优控制率。
2 问题描述
考虑如下非线性系统的动态方程:

2.1 相关的微分几何概念
为了完整的说明状态反馈精确线性化的设计原理,首先给出在推导中使用的一些相关的微分几何概念,包括关系度r和Lie导数的概念。




定理1考虑由系统(2)描述的线性系统关于性能指标(14)的LQR最优控制问题。假设系统完全可观、可控,则系统的LQR最优控制率唯一存在。其表示形式为:

结合式(13)得到系统的最优控制率:

3 控制系统在单连接机器人上的应用
单连接机器人的模型可以表示为:



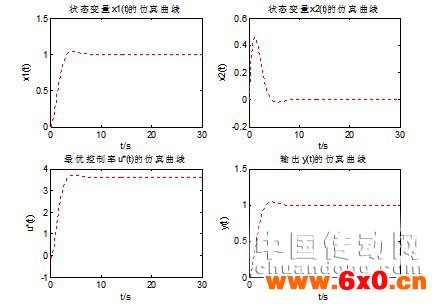
图1 仿真曲线
4 结论
本文针对非线性系统,研究了基于状态反馈精确线性化最优控制器的设计问题,给出了关系度r等于系统阶数n时的非线性系统精确最优控制器的设计方法,最后通过对单连接机器人非线性模型设计基于状态反馈精确线性化的最优控制器,仿真结果表明,本文设计的控制器效果非常好且易于实现。










 QQ交流群
QQ交流群

