引言
随着机器人技术逐渐成熟,机器人作业环境的复杂化,移动机器人在真实的环境中运动并完成指定的任务,机器人的路径规划是首先要解决的问题。所谓的最优路径就是依据某些或某个准则(如行走路线最短、行走时间最短、工作代价最小等),在机器人的工作空间中找到一条从起点到终点的最优或接近最优的路径。
近年来,解决移动机器人在动态未知环境下的路径规划问题一直困扰着人们。对此,国内外许多学者提出了有效的规划算法:如人工势场法,蚁群算法,随机路标图法(PRM),遗传算法等。Tang等提出将动态障碍物在一段时间内看成是静态的,此时路径规划问题就可以用栅格法解决,此法称之为动态栅格法。郭玉把蚁群算法应用在复杂静态环境中,解决了路径规划中的避碰问题,并且提高了路径搜索的效率。槐创锋等针对预测动态障碍物轨迹的问题提出采用自回归模型,经实验证明该模型具有良好的避障能力。
本文采用支持向量回归机模型(SVR)预测动态障碍物轨迹,该模型具有更好的准确性和时效性。人工势场法在实现过程中会有计算复杂度大和运行速度慢的现象,当处于复杂的动态未知环境下时,人工势场法难以达到实时性的要求。本文采用SVR算法与PRM算法结合的方法对机器人进行路径规划时,不需要对工作空间中的障碍物进行精准地数学建模,通过仿真实验证明本文算法具有较好的运行精度和实时性,并且能够有效地解决动态工作空间中的路径规划问题。
1算法描述
1.1支持向量回归机
对于动态障碍物的轨迹趋近于线性的情况下,考虑采用线性回归函数:




表1四种核函数预测误差比较
| t | j(mm2) | m(m) | n(m) | a | R |
| 0 | 22.4133 | 0.0218 | 0.0003 | 0.0050 | 0.9306 |
| 1 | 120.3743 | 0.0194 | 0.0002 | 0.0263 | 0.5974 |
| 2 | 15.4970 | 0.0184 | 0.0001 | 0.0035 | 0.9798 |
| 3 | 21.7410 | 0.0221 | 0.0003 | 0.0047 | 0.9646 |
训练集和测试集的实验流程图如图1所示。
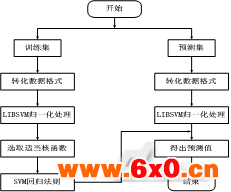
图1训练集和测试集的实验流程图
2.3验证SVR
笔者在Inter(R)Core(TM)Duo-E7500的CPU,内存16G的Linux操作系统下进行实验。由于选取不同的核函数会影响预测的精度,所以需要经过对比实验,选出满足平方相关系数R最大,并同时保证以上几种误差最小的支持向量回归模型。由表1可以看出,当支持向量回归模型选取高斯核函数时预测值与真实值的误差最小。为验证本文算法的优势,可以将本文算法测试后的到的结果,分别与BP神经网络,自回归两种常用的预测算法进行比较。
在预测动态障碍物轨迹的实验中,选同一组数据对以上三种算法进行测试,预测值与真实值的相对误差对比结果如图2所示。
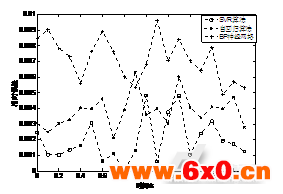
图2相对误差比较实验结果
由图2可知,SVR算法的预测误差较小,BP神经网络的预测效果不好,可能的原因是神经网络算法得到的最优解不一定是全局最优解,有可能只是局部最优解。采用自回归算法的实验结果还不错,但是没有SVR算法的准确度好。
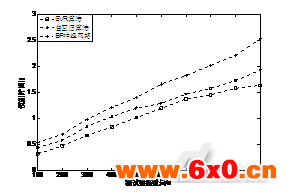
图3时效性比较实验结果
时效性对比结果如图3所示,SVR算法在时效性具有一定的优势,即在一定的时间之内应用SVR算法能更加快速地对动态障碍的轨迹进行预测。
2.3时效性对比试验
通过仿真实验可以证明SVR算法在预测动态障碍物轨迹方面具有一定的优越性,然后对融合SVR的PRM算法与其他算法在路径规划方面进行对比实验。在动态已知环境下,给定初始位置和目标位置,分别用本文算法、蚁群算法、动态栅格法对机器人进行路径规划,对比三种算法的时效性。选取10组不同的初始位置和目标位置,分别对以上算法进行实验对比,对比结果如图4所示。由图4可知,本文采用的SVR算法与PRM算法结合的方法与蚁群算法和动态栅格法比较,本文算法进行路径规划所用时间最短,具有更好的时效性,并且规划的路径最短。
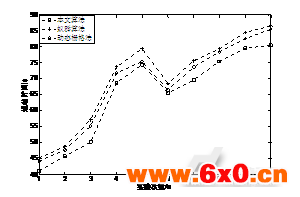
图4时效性实验比较结果
通过实验证明栅格越小,环境信息储存量就越小,规划时间越长,越趋于最优路径,所以时效性和最优路径不能兼顾。蚁群算法虽然具有较好的鲁棒性,但是容易陷入局部最优和规划时间较长的缺点。在给定相同的初始位置和目标位置的情况下,采用本文算法所用的时间最短。
3路径规划
本实验在Inter(R)Core(TM)Duo-E7500的CPU,内存16G的Linux操作系统下进行的。通过把SVR算法和PRM算法进行有机地结合,有效地解决了机器人在动态环境下的路径规划问题。将动态障碍物的位置信息,作为支持向量回归模型的输入。然后采用支持向量回归机模对下一时刻动态障碍物的位置信息进行预测。此时动态障碍物可以看做成瞬间静止的,把问题转化为瞬时静态的路径规划。为寻找该时刻的最优路径,可以采用PRM算法进行路径规划,并且实时更新路径,最终实现从起点到终点的最优路径或近似最优路径。为了证明本文算法的优越性,分别与蚁群算法和动态栅格法进行对比,仿真实验结果如下。
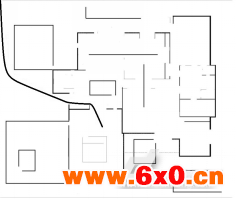
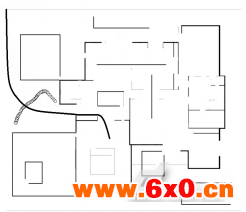
图5蚁群算法在静态环境和动态环境下的路径规划
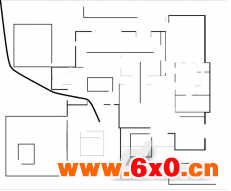
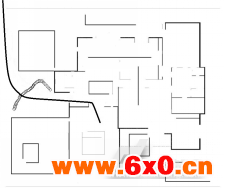
图6动态栅格法在静态环境和动态环境下的路径规划

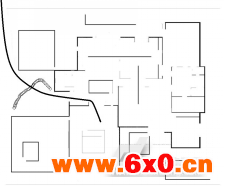
图7本文算法在静态环境和动态下的路径规划
实验在长为17米,宽为15米的仿真环境下进行,如图5、6、7所示,机器人分别在静态和动态环境下采用三种算法进行路径规划的实验结果,三种算法在静态时规划的路径长度分别为16.03m、15.14m、14.73m,动态时路径长度分别为16.85m、16.64m、15.4m。从结果可以看出本文算法规划出的路径最短,时效性更好,不但避免了蚁群算法容易陷入局部最优的缺点,也避免了动态栅格法的环境信息储存量与规划时间难以兼顾的缺点,更趋近于最优路径。
4总结
本文对动态未知环境下移动机器人的路径规划问题进行深入研究分析,并且通过大量的仿真实验验证本文算法的可行性与时效性。利用支持向量回归机算法对动态障碍物的行走轨迹进行预测,把动态路径规划问题转化为静态路径规划问题。然后利用PRM算法对机器人进行瞬时静态的路径规划。两种算法通过有机地结合,为移动机器人在动态环境中找到一条最优或接近最优的无障碍路径。











 QQ交流群
QQ交流群

