柔性臂因其质量轻、结构设计紧凑等优点被广泛应用在航天器、柔性机器人等领域，但是，其末端在运行过程中易产生抖动，严重影响其工作效率和定位精度，甚至危害整个系统的安全。国内外研究人员针对柔性臂的振动抑制问题，提出了PID控制、模糊控制、自适应控制、滑模变结构控制、最优控制等控制方法，对柔性臂振动抑制的反馈控制方法进行了探讨。输入整形技术由Singer和Seering首次提出，被广泛应用于柔性结构的振动抑制，该方法属于前馈控制方法，也是一种独特的振动抑制方法。Youmin等将输入整形技术应用于桥式起重机，抑制抖动的同时也提高了起重机的运输效率；Alsaibie等应用输入整形抑制了液体在运输过程中的晃动；Dhanda等对输入整形器进行改进，设计最优输入整形器有效抑制了起重机的残留振动；Pradhan等将输入整形与自适应控制结合来控制摆动负载的左右晃动。但是输入整形技术在抑制柔性系统振动的同时会导致系统响应时间延迟，严重降低系统的工作效率。
本文针对输入整形技术引起的响应时间延迟问题，基于最优控制理论设计最优输入整形器以减小系统的响应时间，并将最优输入整形器与模糊PID控制器结合进行柔性臂的振动抑制。
柔性臂动力学模型
绕伺服电机转轴旋转运动的柔性臂机械结构和物理模型如图1所示。图1(a)中，伺服电机转轴与转盘连接，柔性臂的一端通过转盘夹头连接在电机转轴上，质量块附于另一端，基座用于固定整个实验平台。
图1(b)中，设以电机转轴中心O为原点建立惯性系XOY和体坐标系xOy，柔性臂的弹性模量为E，横截面对中性轴的惯性矩为I，密度为，截面面积为A，长度为l，末端质量块质量为ml，伺服电机转轴、转盘的转动惯量之和为J0，柔性臂运动所对应刚体转角为θ(t)，转轴输入控制力矩为u(t)。
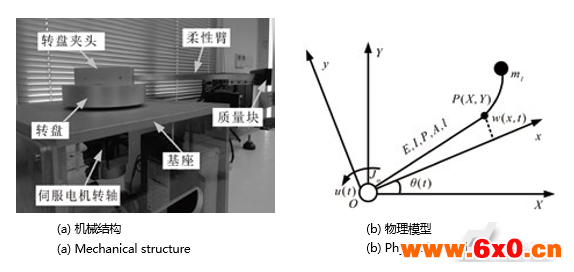
图1柔性臂机械结构与物理模型
假设柔性臂横向振动远大于轴向振动且横向振动较小，根据振动力学原理，柔性臂可视为Euler-Bernoulli梁。设P(X,Y)为时刻t的柔性臂上任意一点的坐标，w(x,t)为P点在坐标系xOy下的横向弹性振动位移，根据Euler-Bernoulli梁的振动理论，均匀材料等截面柔性臂的弯曲自由振动微分方程为
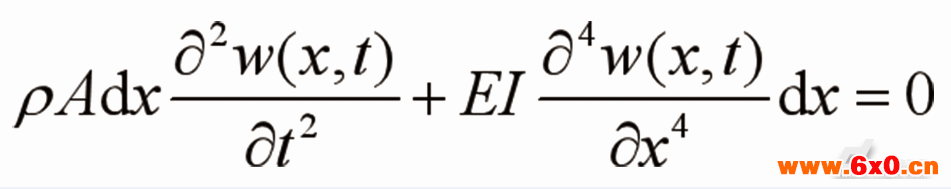(1)
由假设模态法，设
(2)
式中，Wi(x)为柔性臂在x处的振型函数或模态函数，qi(t)是相应振型的幅值，称为模态坐标。
定义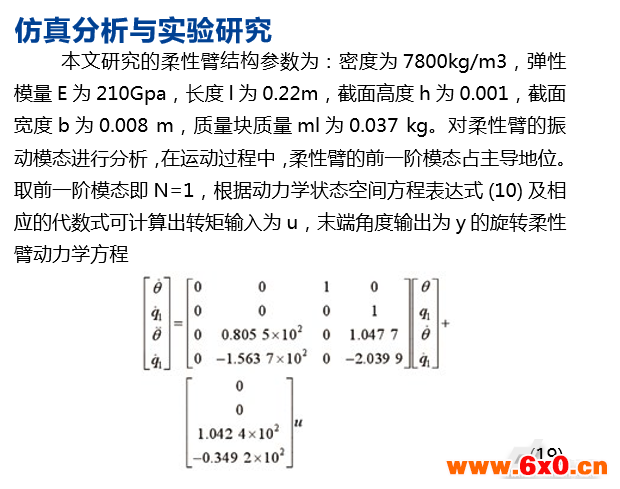
，根据柔性臂的四个边界条件
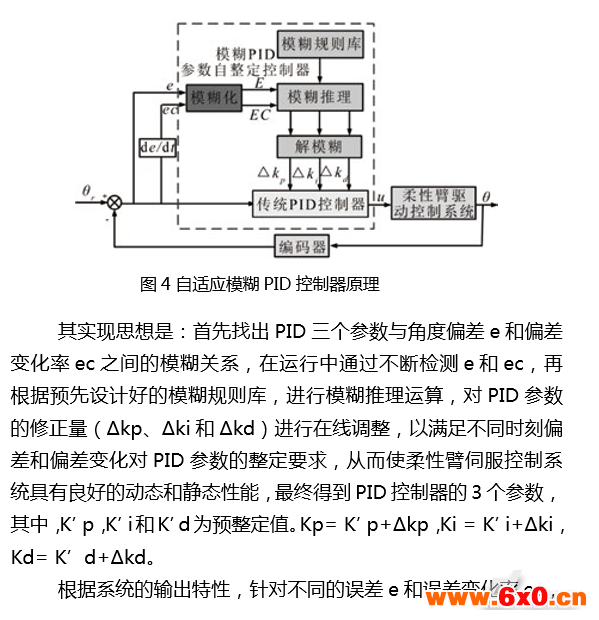
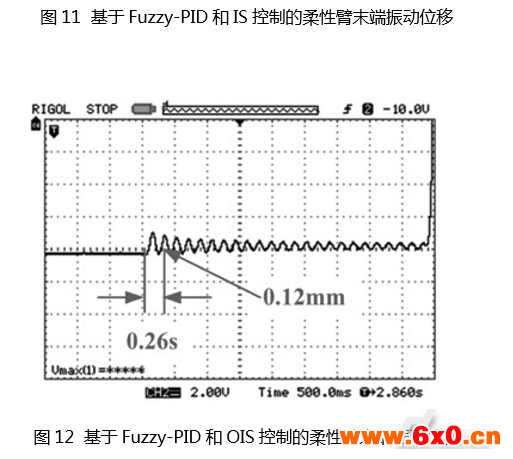
图9柔性臂振动抑制的实验平台
QQ交流群
