复杂的交通状况和发动机的转动带给汽车的冲击和多维振动将会严重影响车载设备的性能。车体运动带来的振动是不可能被完全消除的,因此通过隔振设备减弱振动能量从车体向车载设备的传递是最为有效的方式。车体的振动是多维的,根据隔振系统与振源自由度相一致的原则,隔振系统的自由度应与车体的振动自由度相同。由于多维振动隔离是通过在隔振机构中添加隔振单元实现的,因此其性能完全由振动隔离机构和其控制策略决定。
并联机构由于其高静态刚度、低惯性和高灵活度等优势的存在使其成为多维隔振系统主体机构的良好候选。Gouig-Stewart平台、Hexapod平台已经被广泛地应用于精密系统的六维隔振系统中。而以并联机构为主体的多维隔振系统近年来更是得到了迅速发展,特别是基于MR(Magnetorheological)阻尼器的系统。在此类隔振系统中,控制策略是影响系统性能的重要因素。在最近20年中,大量的理论和实验研究表明半主动控制策略具有良好的隔振效果和比较小的成本,但是其隔振效果受到控制策略的影响较大。一般在半主动控制策略中必须考虑如何得到最优控制力和MR阻尼器的实际输出力两个方面。本文中采用了基于基因算法的模糊模型计算得到MR阻尼器的输人电流以避免求解高非线性模型,并基于车载设备的振动特点提出了一种基于3-RPC并联机构的三维隔振系统,介绍了系统的运动学和动力学模型,提出了一种基于MR阻尼器的半主动控制策略,最后,加工制造了一套实验样机并通过实验验证了隔振系统的有效性。
隔振系统模型
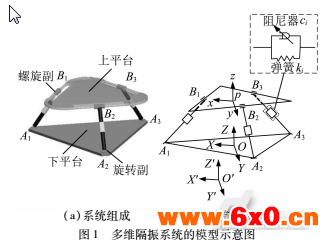
本文提出的隔振系统用来隔离从车体传递到车载设备(如车载机器人系统等)的振动信号。根据车载设备的振动特点,文中提出的隔振系统具有三个平移自由度,系统的主体机构为一个3-RPC并联机构。该系统由下平台、上平台和三个独立的支链组成(见图1(a)。在每一个支链中有一个弹簧一阻尼器隔振子单元,如图1(b)所示,其中k为弹簧刚度系数,c为阻尼器的阻尼系数。支链用A、B表示,每个支链的底端与下平台通过一个旋转副连接于点A,而上端则通过一个圆柱副与上平台相连于点B。A和B均对称布置于各自所处的平面内,且每个支链的旋转副和圆柱副的轴线是相互平行的。根据螺旋理论,3-RPC机构的每一个分支可以提供两个共面的约束力偶,它们的轴线与旋转副的轴线垂直。由于三个分支提供的约束力偶限制了上平台的空间转动自由度,因此它只具有三个平移自由度。为了更好地实现三维振动隔离的目标,通过将机构在工作空间内所有自由度上的固有频率和的最大值作为极小化目标,同时考虑工作空间、灵巧度以及运动副转角范围等实际约束条件对系统的几何尺寸进行了优化:PB为150mm,OA为400mm,平面的初始高度为245mm。
运动学和动力学建模
在图1(b)中,0'(X',Y',Z')是建立在地面上的笛卡尔坐标系,0'3X,Y,Z}为下平台坐标系,动坐标系P{x,y,z}处在上平台的几何中心点P上。为了简化建模过程并不失一般性,三个坐标系的轴线在初始位置是相互平行的。
1.雅可比矩阵
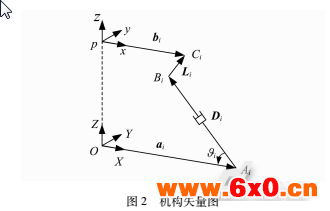
并联机构的运动学分析包括逆解、速度和加速度分析等部分。由于并联机构的运动学分析相对简单,因此文中将不再详细叙述,而只给出系统的雅可比矩阵。建立雅可比矩阵时所使用的是环路方程法。如图2中所示,根据环路方程法可以得到机构的逆雅可比矩阵为

2.动力学建模
系统的闭环动力学方程是通过牛顿欧拉方程建立的。由于动力学建模的过程比较繁琐,本文将不再详细描述而只给出系统的动力学模型,更加详细的建模过程请参照相关文献。
在建模过程中忽略杆的转动惯量和速度二阶小量,可以得到机构的闭环动力学模型如下:
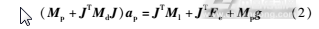
3.多维隔振系统的半主动控制
(1)隔振系统控制模型
如果在式(2)所表达的动力学模型中弹簧的初始变形可以抵消所有的静态重力,那么在动力学模型中消除静平衡项后可以整理得到系统的振动模型为:
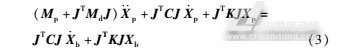
式中:Xp,Xb为上平台、下平台的位移矢量;C、K为阻尼矩阵、刚度矩阵,且C=diag(c1czc3),K=diag(k1kzk3)。
在振动模型的基础上可以得到系统的控制模型,其中上平台的平移加速度作为系统的控制目标,而下平台的平移速度作为系统的扰动信号。由于状态变量反馈能够全面地反映控制系统的内部特性,因此本文采用状态反馈实现隔振平台的振动控制。文中以上平台与下平台间的相对位移和上平台速度作为状态反馈量。另外,MR阻尼器的逆模型中要用到阻尼器两端的相对速度信号,此信号可以通过上下平台的相对位移进行微分,然后再通过雅可比矩阵求解的方式得到。在实际控制过程中,MR阻尼器的出力大小是受限的,因此MR阻尼器的控制信号也应该受到合理的约束。在控制系统中的变量和扰动量为:
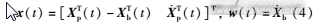
系统的动力学状态方程和被调输出方程所组成的控制系统模型可以表示为:
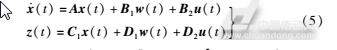
另外,由于MR阻尼器的输出力受到一定的限制,所以在控制器的设计过程中还需要考虑如下条件的限制:
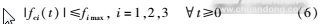
(2)隔振系统的半主动控制策略
本文所设计的隔振平台的半主动控制算法包括三个步骤:计算最优控制力、计算各支链MR阻尼器可能实现的输出力、计算各MR阻尼器的输人电流。考虑到此三点要求以及本文中隔振平台的实际结构,文中提出了一种模糊最优控制策略实现平台的振动控制。
在此策略中,通过H二状态反馈控制策略得到各个支链中的最优控制力,然后根据支链中的运动状态并基于MR阻尼器的工作机理得到各个支链中MR阻尼器的可达输出力,最后通过模糊模型得到各个MR阻尼器的输人电流。具体控制流程如图3所示。
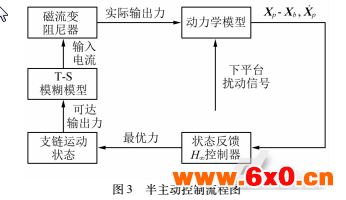
其中在计算MR阻尼器的输人电流时采用了基于遗传算法的进化Takagi-Sugeno模糊模型。由于MR阻尼器的动力学模型具有高度的非线性,因此如果直接求解MR阻尼器的动力学逆模型,根据运动状态和输出力得到输人电流,会因为求解强非线性方程而使计算量剧增、效率低下。而解决高度非线性问题是模糊控制的一大特点,通过此控制方法既可快速逼近MR阻尼器的逆模型,又可避免控制力超调。由于篇幅限制,本文将不再详细介绍基于模糊模型的MR阻尼器输人电流辨识方法,更多细节可参考文献。
实验与分析
作为一个面向工程应用的系统,实验是验证其性能的最可靠途径。所以,文中设计与制造了一套实验样机原型,建立了软硬件控制系统。然后在现有实验条件下对系统分别进行了不同方向上的随机信号和正弦信号输人时的振动响应实验。实验结果表明该系统具有良好的隔振效果。
1.实验方案设计
由于实验条件所限,文中分别对系统的水平和垂直方向的隔振性能进行了验证。实验方案主要包括以下几个步骤:
(1)单向正弦扫频实验。
将隔振平台的下平台与振动台相连,分别在X和Z方向上进行正弦信号扫频实验,并记录上下平台的加速度。此实验主要寻找系统在各个方向上的固有频率,并验证平台在频域范围内的隔振性能。
(2)单向随机振动实验。
将隔振平台的下平台与振动台相连,分别在X和Z方向上进行随机信号振动实验,并记录上下平台的加速度。本实验分被动控制和半主动控制两种模式分别进行。此实验主要验证隔振平台在随机信号激励下的隔振效果,并对被动控制和半主动控制效果进行比较。
(3)单向定频正弦实验。
分别在X和Z方向上进行定频正弦信号实验,激励频率分别为平台在此方向上的固有频率。实验分被动控制和半主动控制两种模式进行。此实验主要验证隔振平台在遭遇具有固有频率信号时的隔振能力。
2.振动实验与结果分析
实验过程如图4所示。图4(a)为水平振动实验,图4(b)为垂直振动实验。

(1)单向正弦扫频实验
正弦扫频实验的主要目的是为了寻找隔振系统在各个方向上的固有频率,因此在此实验中并未对MR阻尼器进行控制,而是在MR阻尼器的零场阻尼下进行的。由于汽车的一阶固有频率一般低于5Hz,因此在实验中采用的振动台扫频范围为1-0Hz,在1-5Hz采用定幅扫频,台面振幅为20mm,5-20Hz采用定加速度扫频,加速度为2g,扫描速率为1OCT/min。
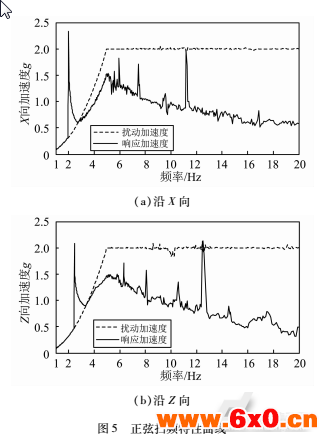
在实验过程中发现,当振动实验台分别在X轴或Z轴方向上施加激励时,在其它非激励方向上均能测量到运动信号,这主要是由于并联机构的藕合运动引起的。在式(3)所给出的振动模型中,系统的质量矩阵、阻尼矩阵和刚度矩阵均为非对角阵,因此系统在各个方向上的平移运动是相互藕合的。在X方向和Z方向分别进行正弦扫频振动实验时,所采集的样机上平台的加速度频域特性曲线如图5所示。从图5可知,振动台在两个方向上的振动曲线
走势基本相同:在扫频开始阶段,上平台的加速度与激励加速度基本相同;随着扫频信号频率的增大,上平台的加速度突然上升,系统发生共振;而在扫频频率越过共振区后,上平台振动加速度比激励加速度要小,说明隔振系统起到了隔离振动传递的作用。
(2)单向随机振动实验
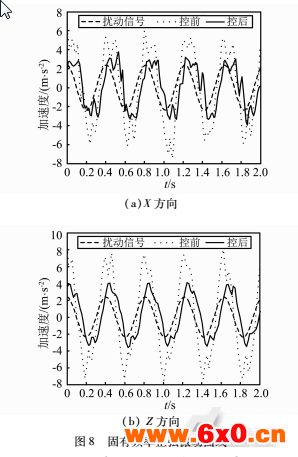
随机振动实验是检验隔振平台实际隔振能力的重要方式。虽然隔振系统在水平面内各个方向的振动性能不同,但是通过前文的理论分析和仿真可知,水平面内每个方向上的振动特性的基本趋势大致相同,因此本文仅选择了轴X和轴Z两个方向进行了随机振动实验。通
过参考国家标准给定的路面功率谱密度函数,假设汽车在B级路面上行驶,实验中所采用的振动信号频率范围为1-20Hz,加速度功率谱密度为0.05(m/sz)Z/Hz。
(3)单向正弦定频振动实验
此实验为了验证隔振平台在各个方向上受到具有平台固有频率的信号扰动时的性能。实验中振动台所输出的正弦信号振幅为10mm,扰动信号频率为扫频实验中得到的系统在各个方向上的一阶固有频率。图6为隔振平台受到具有固有频率的正弦信号扰动时的上平台的响应加速度。由图中可知,在被动模式下,此时平台将达到共振,响应加速度放大3倍左右;而当采用本文提出的半主动控制策略时,虽然响应加速度仍然比扰动加速度要大,但是相比
于被动隔振时有明显的下降。










 QQ交流群
QQ交流群

