摘要:为了实现SCARA机器人的高速高精度控制,将带偏心负载的SCARA机器人简化成三连杆机构,并建立机构的惯性力模型,进行辨识计算出机器人各惯性项系数的值,建立基于惯性力模型的加速度自适应控制方法,自适应计算关节一理论最大运动角加速度。通过实验研究和分析,加速度自适应控制方法能够充分发挥机器人电机的机械性能,防止电机因电流过大而报警,该方法能较好地应用于SCARA机器人的工程控制中。
1引言
工业机器人(后文统称机器人)已广泛应用于现代工业,随着机器人和自动化技术的发展,其高速运动时的准确性和稳定性日益成为检验机器人性能的重要指标,是机器人的运动控制系统必须考虑的因素。在高速运动的情况下,机器人的非线性控制特性十分明显,并且实际存在的各种复杂不确性因素也严重影响着机器人的控制精度。SCARA(SelectiveComplianceAssemblyRobotArm)机器人广泛应用于3C装配、抓取等对机器人的运动速度和精度要求更高的场合,因此对SCARA机器人进行优化控制方法研究,以实现高速高精度的控制目标具有重要的理论意义和实用价值[1-3]。
为了实现机器人的高速高精度运动控制,国内外的研究主要集中在以下几个方面:(1)智能控制方法,主要包括时间最优[4]、能量最优[5]、加加速度最优[6]等,以上智能寻优算法,主要是对某些特定的轨迹,根据机器人关节几何、速度和加速度等约束条件下,建立机器人运动时的关于时间、能量、加加速度等的目标函数表达式,采用智能寻优的方法计算最优解。(2)基于动力学模型的控制方法,通过机器人动力学参数辨识,得到机器人的逆动力学模型,这样,可以根据目标轨迹计算出目标轨迹各处的理论驱动力矩,再进行相应的动力学控制。
综合来看,智能控制方法因为计算时间周期的原因,容易造成机器人控制器内存资源的紧张,很难应用在复杂的工业环境和实时插补的场合;基于动力学模型的运动控制,需要先进行复杂的动力学参数辨识,对模型的精确度要求较高,且需要计算每个插补周期的理论驱动力矩值,计算量较大。
本文在实时开放式SCARA机器人控制平台上,根据SCARA机器人的特点,建立简化的关节惯性力模型;通过数据采集和处理,辨识出模型各系数的值;根据机器人基关节(关节一)电机的理论最大电流,自适应计算插补路径起点处的加速度和终点处的减速度。这样,在开始插补前,可以确定最大的机器人关节运动加减速度,最大程度地利用关节一电机的机械性能,提高机器人运行的速度和精度。实验结果表明该方法能较好地适用于SCARA机器人的高速高精度运动控制中。
2基于惯性力模型的SCARA机器人加速度自适应控制方法
2.1SCARA机器人惯性力建模
串联机器人的动力学方程可以表示为:
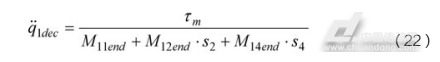 (1)
(1)
式(1)中, 为各关节的驱动力矩,
为各关节的驱动力矩,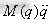 为惯性力项,
为惯性力项,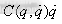 为哥氏力和离心力项,
为哥氏力和离心力项,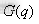 为重力项。对于主要应用于平面抓取、码垛等领域的SCARA机器人,其高速运动时受力较大的主要是关节一。所以考虑关节一的动力学表达式时,可以忽略重力项的影响,而只考虑惯性力、哥氏力及离心力的作用。为了实现高速控制,一般将关节角加速度设置为角速度的10倍以上,这样造成惯性力的作用远大于离心力和哥氏力。
为重力项。对于主要应用于平面抓取、码垛等领域的SCARA机器人,其高速运动时受力较大的主要是关节一。所以考虑关节一的动力学表达式时,可以忽略重力项的影响,而只考虑惯性力、哥氏力及离心力的作用。为了实现高速控制,一般将关节角加速度设置为角速度的10倍以上,这样造成惯性力的作用远大于离心力和哥氏力。
图1所示为典型的SCARA机器人高速运动时,关节一电机速度、加速度和电流(与力矩呈比例关系)分布曲线图:
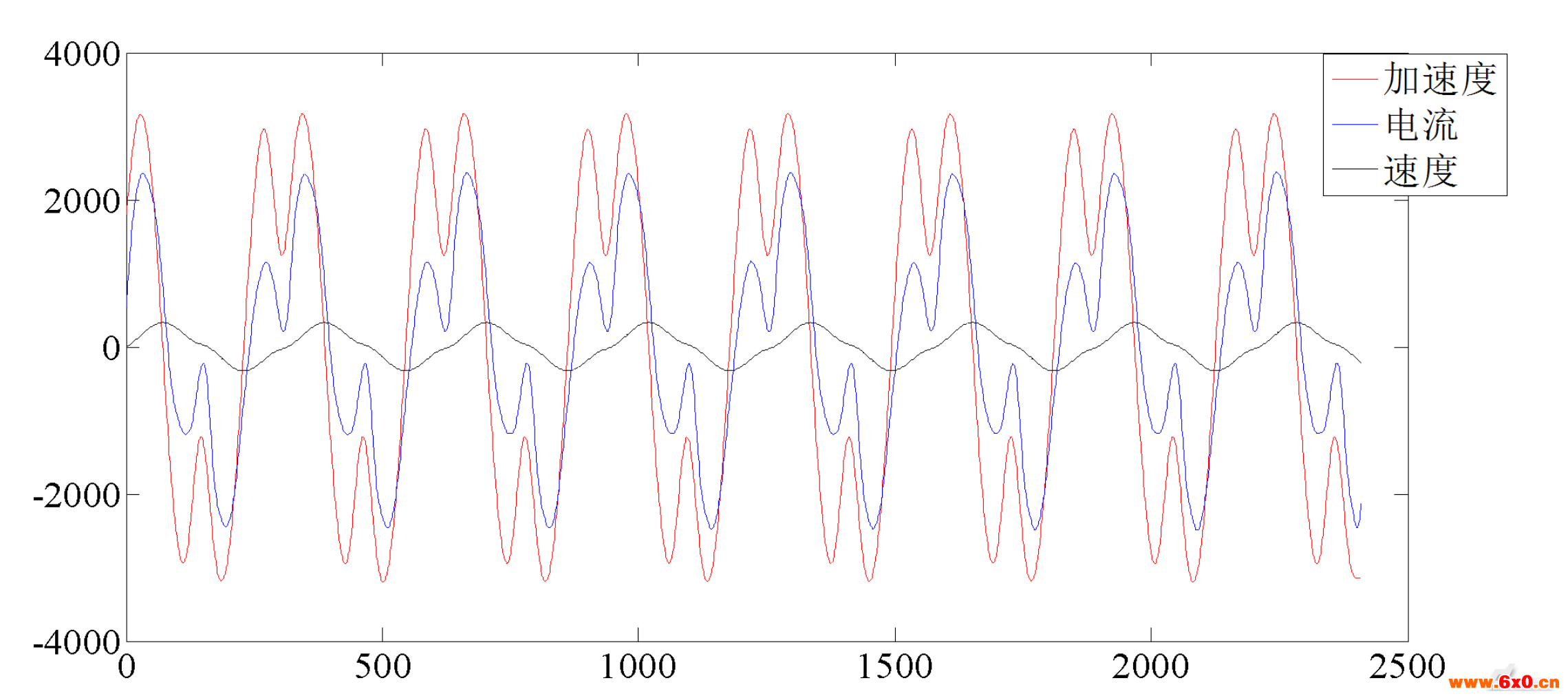
图1典型的机器人运动时关节一电机速度、加速度和
电流分布曲线图
Fig.1Typicaldistributioncurveofmotorspeed,accelerationandcurrentofjoint1whenrobotmoves
图1中,横坐标为插补时间,单位是ms,黑色曲线为电机一速度曲线,单位为°/s,蓝色曲线为电机一加速度曲线图,单位为°/s2,红色曲线为电机一电流曲线图,单位为mA。从图一可以看出,电流曲线的变化趋势, 基本与加速度曲线的变化趋势重合,因为式(1)中各项只有惯性力项与关节角加速度项 相关,所以SCARA机器人进行高速运动时,惯性力矩在关节驱动力矩各项中占据主导作用,建立机器人的惯性力模型并进行基于模型的控制可以达到很好的控制效果。
相关,所以SCARA机器人进行高速运动时,惯性力矩在关节驱动力矩各项中占据主导作用,建立机器人的惯性力模型并进行基于模型的控制可以达到很好的控制效果。
对于如图2所示的带偏心负载的SCARA机器人,其主体结构类似于一个简化的平面三连杆模型,如图3所示。
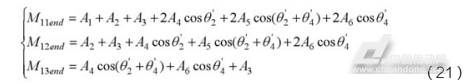
图2带偏心负载的SCARA机器人
Fig.2SCARArobotwitheccentricload
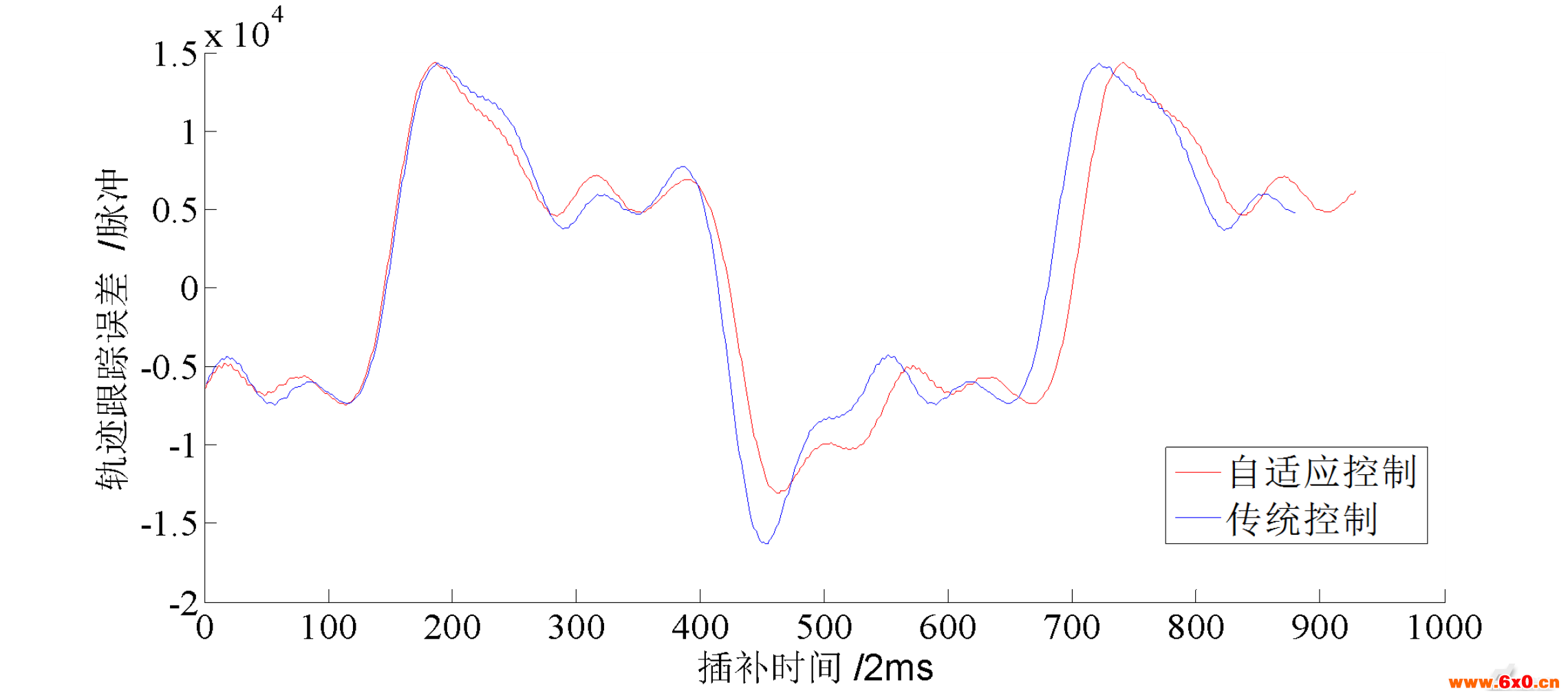
图3简化的平面三连杆SCARA机器人模型
Fig.3AsimplifiedplanarthreelinkSCARArobotmodel
图3中,m1和m2分别为SCARA机器人大臂和小臂的质量,l1和l2分别为机器人大小臂的长度,d1和d2为连杆质心位置,d4为机器人末端所挂负载的偏心量,负载质量为m4,为各连杆的转角。使用拉格朗日方程[7],进行动力学方程推导:
 (2)
(2)
式(2)中,k为系统的总动能,u为系统的总势能,通过式(2)推导可以得到,在只考虑惯性力的情况下,第一关节的动力学表达式为:
 (3)
(3)
式(3)中,分别为机器人动力学方程质量矩阵的第一行三个元素,三项的数学表达式分别为:
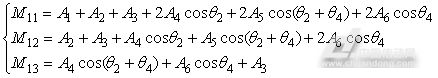 (4)
(4)
其中:
 (5)
(5)
式(5)中, 分别为大小臂及负载的转动惯量。在实际机器人的控制应用时,在(4)式和(5)式中,各关节转角
分别为大小臂及负载的转动惯量。在实际机器人的控制应用时,在(4)式和(5)式中,各关节转角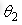 和
和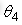 是可以精确已知的,在负载质量和负载偏心一定的情况下,A1至A6等参数的值均为一定的,可以通过动力学参数辨识进行辨识计算得到。
是可以精确已知的,在负载质量和负载偏心一定的情况下,A1至A6等参数的值均为一定的,可以通过动力学参数辨识进行辨识计算得到。
2.2惯性力模型的动力学参数辨识
传统的机器人动力学参数辨识方法,需要首先离线优化计算一条复杂的激励轨迹[8],一般使用多次多项式或傅里叶级数进行关节轨迹激励;然后使机器人运行激励轨迹,通过大量的数据采集和处理,最后解超静定方程组得到动力学参数的值。这里,结合SCARA机器人的特点,采用一种简易的方法进行以上参数的辨识。
根据前面的分析可以知道,在SCARA机器人进行关节点位运动时,惯性力矩在关节力矩中占主导作用,特别是在关节角加速度最大处,根据式(3),采用以下方法进行数据采集:
(1)在一定的关节二转角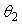 和关节四转角
和关节四转角 下,以最快的速度只动关节一,采集关节一电机的电流和编码器值信息;在不同的
下,以最快的速度只动关节一,采集关节一电机的电流和编码器值信息;在不同的 和
和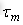 下,重复以上操作,采集5-10组数据。此时,(3)式中只有
下,重复以上操作,采集5-10组数据。此时,(3)式中只有 起作用,对采集的数据进行数据处理,可以建立关节一最大角加速度和最大驱动力矩(和电流呈线性比例关系)之间的数学表达式关系,即:
起作用,对采集的数据进行数据处理,可以建立关节一最大角加速度和最大驱动力矩(和电流呈线性比例关系)之间的数学表达式关系,即:
 (6)
(6)
(2)在一定的关节一转角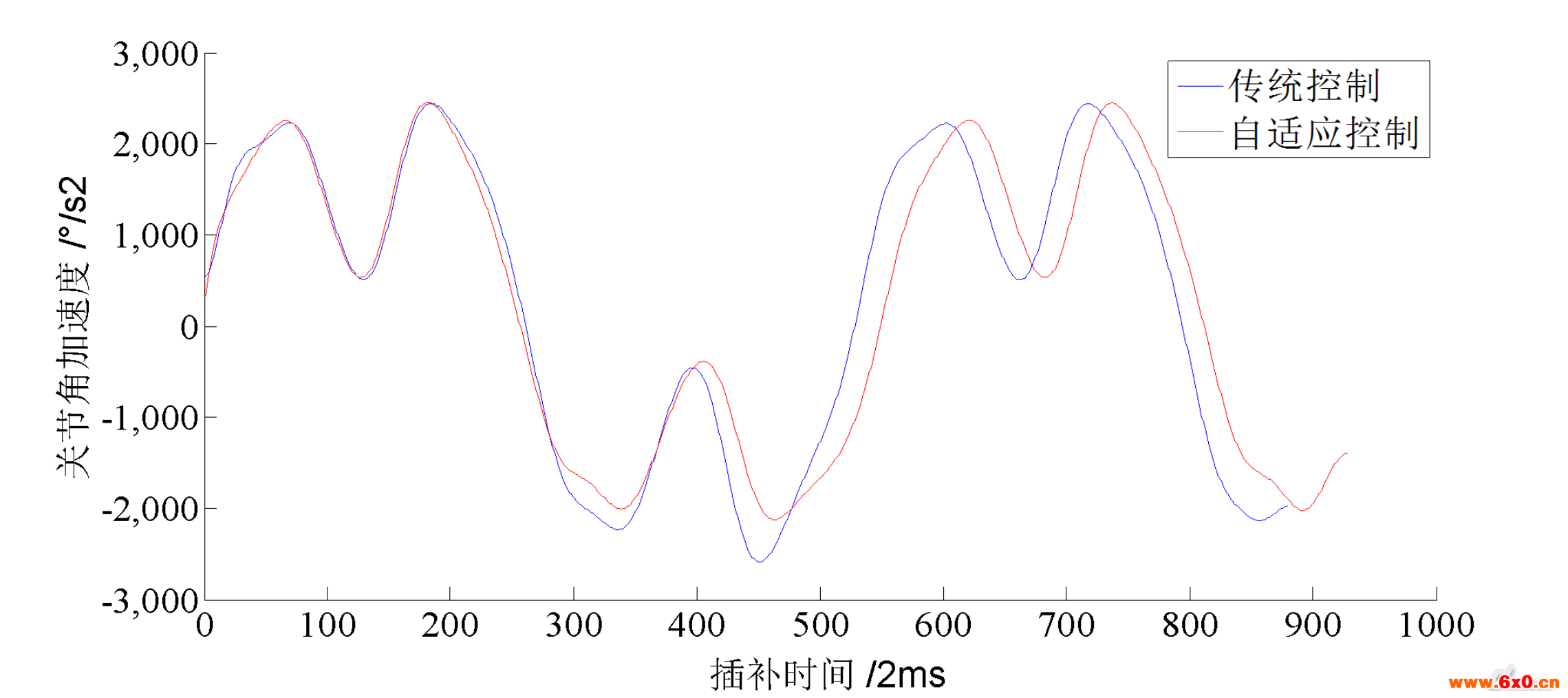 和关节四转角
和关节四转角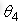 下,以最快的速度只动关节二,采集关节一电机的电流和关节二电机的编码器值信息;在不同的
下,以最快的速度只动关节二,采集关节一电机的电流和关节二电机的编码器值信息;在不同的 和
和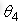 下,重复以上操作,采集5-10组数据。此时,(3)式中只有
下,重复以上操作,采集5-10组数据。此时,(3)式中只有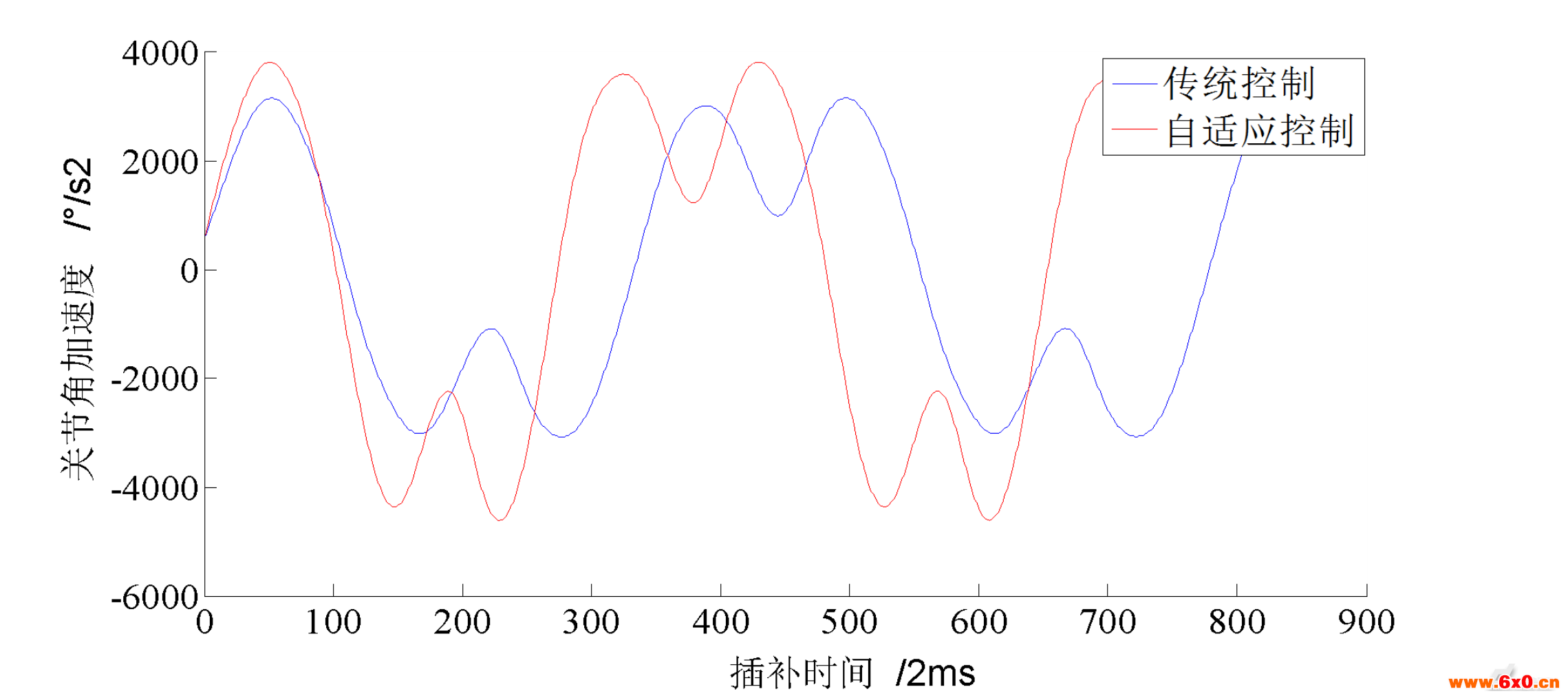 起作用,同理,可以建立关节二最大角加速度和关节一最大驱动力矩之间的数学表达式关系,即:
起作用,同理,可以建立关节二最大角加速度和关节一最大驱动力矩之间的数学表达式关系,即:
 (7)
(7)
(3)在一定的关节一转角 和关节二转角
和关节二转角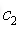 下,以最快的速度只动关节四,采集关节一电机的电流和关节四电机的编码器值信息;在不同的
下,以最快的速度只动关节四,采集关节一电机的电流和关节四电机的编码器值信息;在不同的 和
和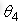 下,重复以上操作,采集5-10组数据。此时,(3)式中只有
下,重复以上操作,采集5-10组数据。此时,(3)式中只有 起作用,同理,可以建立关节四最大角加速度和关节一最大驱动力矩之间的数学表达式关系,即:
起作用,同理,可以建立关节四最大角加速度和关节一最大驱动力矩之间的数学表达式关系,即:
 (8)
(8)
数据采集完成后,要进行数据处理,因为采集的数据是电机的编码器值和电流值,要带入(6)-(8)式中进行方程组求解,必须根据编码器值,采用差分的方法计算关节角加速度,因为两次差分得到的加速度噪声太大,且采集的电流值也存在很大的高频噪声,所以还要采用相应的滤波方法对采集的数据进行处理。
首先,差分计算天然地具有噪声放大的作用[9],关节位置的直接前向差分会放大高频噪声的幅值,使得到角速度和角加速度产生波形失真,影响关节角加速度计算的精度。这里,根据电机编码器值,采用中心差分法,每次计算五个点中中间点的关节角加速度值。
设定五个插补点的时间间隔为T(即机器人的理论插补周期),设第三个点的关节转角时间序列为T(根据关节编码器值计算得到),则其他几个点的时间序列分别为 。分别对
。分别对 进行泰勒四阶展开,并相减可以得到:
进行泰勒四阶展开,并相减可以得到:

式(9)和(10)中,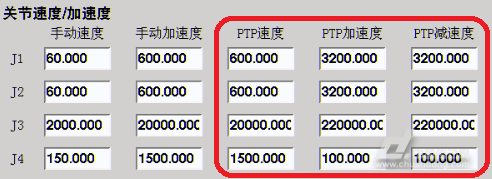 和
和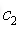 是常数,(9)式乘以8减去(10)式得:
是常数,(9)式乘以8减去(10)式得:
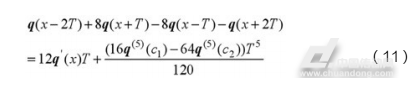
总可以找到一个常数 ,使得式(12)成立。
,使得式(12)成立。

这样,通过采集的机器人运动时各时间序列的编码器值,根据式(9)-式(15),每次依次计算五个点中间点的关节角加速度值,即可以得到机器人运行各时间序列的关节角加速度值。
通过中心差分得到各时间序列的关节角加速度值,仍然会有很多高频噪声,同时,通过伺服电机底层采集的电流值,不经过滤波也会有很大的计算误差。所以,在MATLAB中构建低通巴特沃斯滤波器[10],它可以减小滤波过程中的相位偏移。分别对采集和处理的数据进行依次滤波处理。滤波处理的顺序为:关节转角、关节角速度、关节角加速度、电流值。
经过数据处理后,可以得到关节力矩和加速度值,取机器人每次运动时的最大关节角加速度值和最大力矩,分别带入式(6)-式(8),因为方程组的个数大于未知量的个数,所以采用最小二乘法,辨识计算得到惯性力模型的A1到A6各项参数的值。
2.3基于惯性力模型的SCARA机器人加速度自适应控制
在SCARA机器人进行快速关节点位运动时,因为关节加速过程主要在路径起始和终止段,此时机器人可能会因各关节电机(特别是关节一)所需的驱动力矩过大而报警,特别是在机器人高速重载启停时。这样,可以根据关节一极限力矩的大小,通过惯性力模型和机器人关节点位运动起终点的位姿,自适应计算关节一运动的加速度和减速度,以充分发挥电机的动力学性能,同时保证电机不因驱动力矩过大而报警。
设定机器人运行的起终点分别为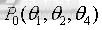 和
和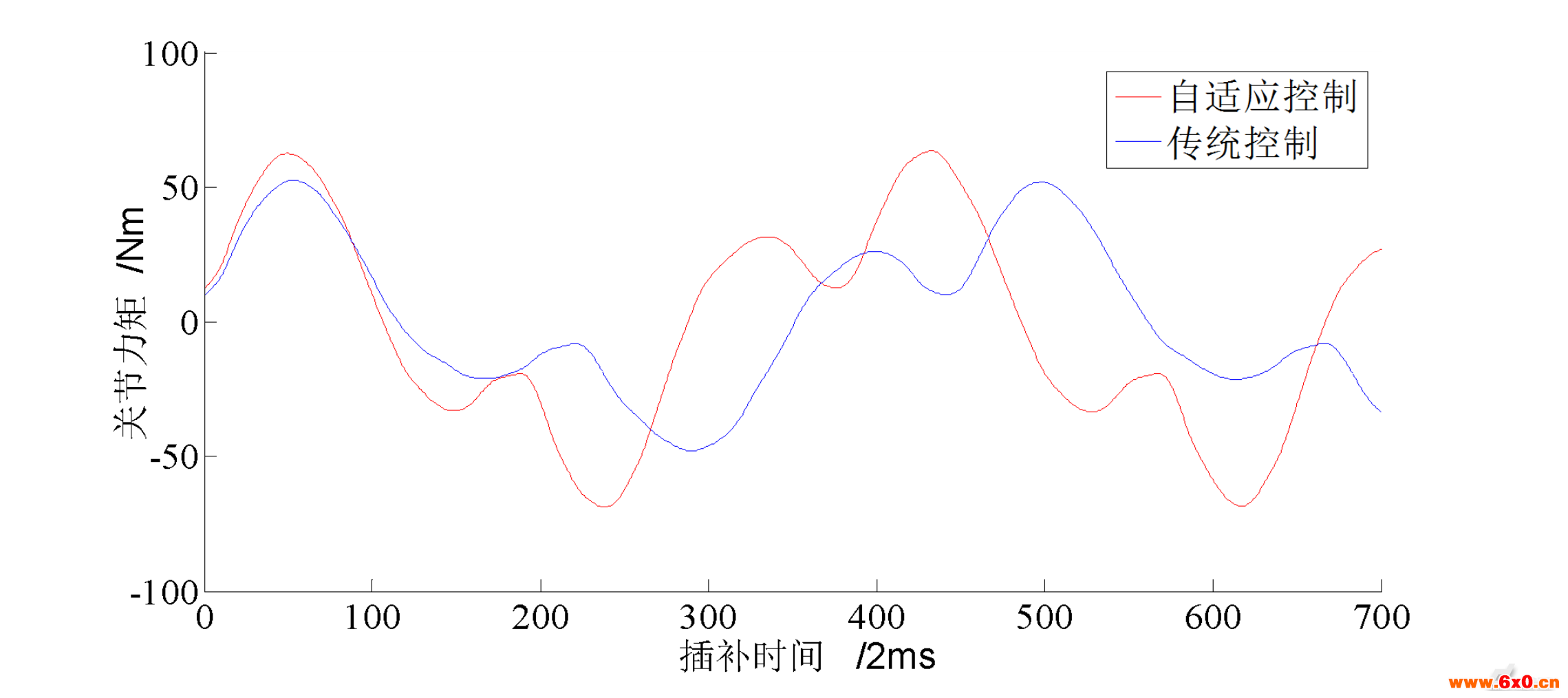 ,因为SCARA机器人的关节三为垂直上下运动,对关节一力矩的影响可以忽略不计,所以没有考虑进来;设定根据关机一电机极限电流计算的关节一极限驱动力矩为
,因为SCARA机器人的关节三为垂直上下运动,对关节一力矩的影响可以忽略不计,所以没有考虑进来;设定根据关机一电机极限电流计算的关节一极限驱动力矩为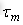 。
。
在已经通过辨识计算,得到惯性力模型的A1到A6各项参数的值后,在机器人运行路径的起点P0处,将 分别带入式(4),可以得到路径起点P0处的质量矩阵中与关节一驱动力矩相关的三项
分别带入式(4),可以得到路径起点P0处的质量矩阵中与关节一驱动力矩相关的三项 分别为:
分别为:
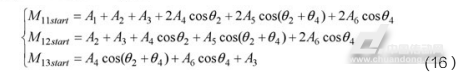
因为SCARA机器人进行关节点位运动时,关节一最大加速度和最大力矩出现的时间序列接近于路径起点处,所以可以近似使用起点处的质量矩阵项,作为最大关节力矩处的质量矩阵项,将式(16)带入式(3),则:
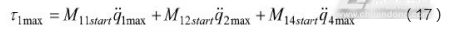
在机器人进行关节点位运动时,为了保证各关节同时启停,各关节实际运动的加速度的比例关系是确定的,设定:

以关节一的极限力矩值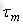 ,作为(19)式中的
,作为(19)式中的 ,则可以计算得到理论最大的关节一运动角加速度值为:
,则可以计算得到理论最大的关节一运动角加速度值为:
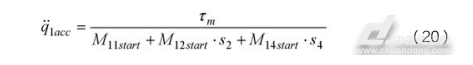
同理,可以得到路径终点P1处的质量矩阵中与关节一驱动力矩相关的三项 分别为:
分别为:
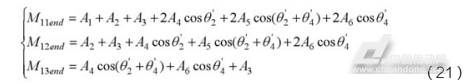
同时,可以得到路径理论最大的关节一减速度为:
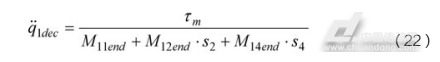
这样,在确定了起终点位姿的情况下,可以根据关节一的极限力矩,在插补开始之前,自适应规划出关节一的理论最大关节角加速度和减速度,既可以保证机器人不因电机电流过大而报警,同时也满足机器人高速运动的要求。
3实验研究与分析
3.1实验平台
实验平台选用的是基于开放式控制器系统的SCARA机器人平台,它通过高速DSP满足实时插补的要求,其控制系统基于ARM+DSP架构,上位机程序运行在ARM端,主要用于机器人示教点的选取及示教程序的编写等功能的实现,机器人的运动控制程序运行在DSP端。ARM和DSP端通过中断中的双口RAM进行数据交互,示教程序通过中断从ARM端传到DSP端,同时在机器人运行的过程中,电机的信息(如编码器脉冲和电流值等)也会实时通过DSP中的中断反馈到ARM端再保存。机器人控制系统框图如图4所示
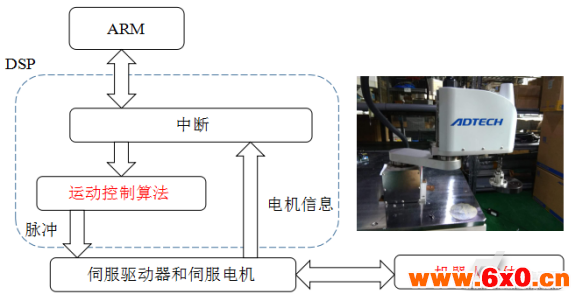
图4机器人控制系统框图
Fig.4Theblockdiagramofrobotcontrolsystem
3.2实验研究与分析
根据文献[11]建立SCARA机器人坐标系,确定机器人连杆参数如下: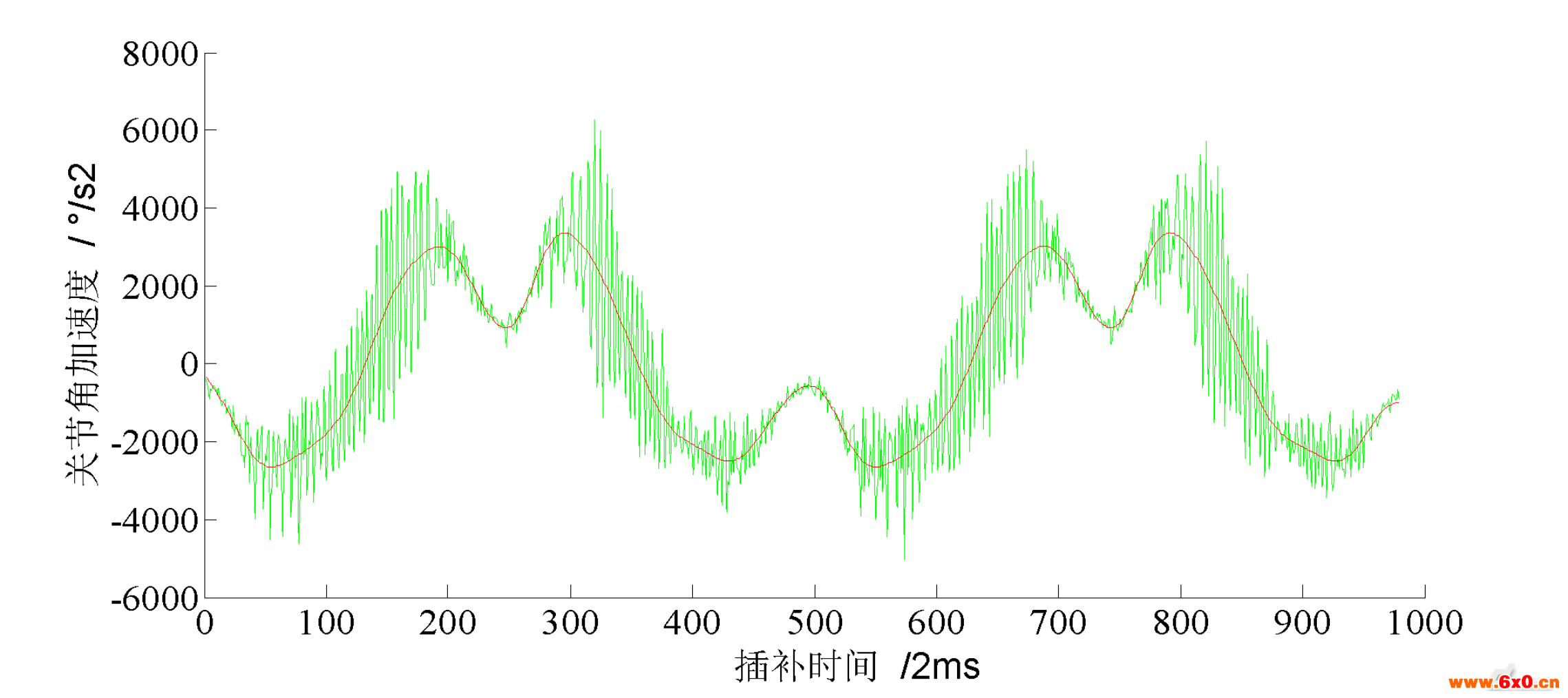 ,机器人携带2kg、60mm偏心负载。
,机器人携带2kg、60mm偏心负载。
首先,根据前述的参数辨识方法,通过数据采集和数据处理,辨识出式(5)中惯性力模型的A1到A6各项参数的值。
在辨识时,选取一组机器人运动数据,对关节电机力矩采用截止频率为10Hz的巴特沃斯低通滤波器进行滤波,对于电机编码器值,在每次差分前后,采用20Hz巴特沃斯低通滤波器进行滤波,再进行数学运算转化为关节角加速度值,图5和图6分别是关节力矩和角加速度的滤波效果对比(绿色为滤波前曲线,红色为滤波后曲线):
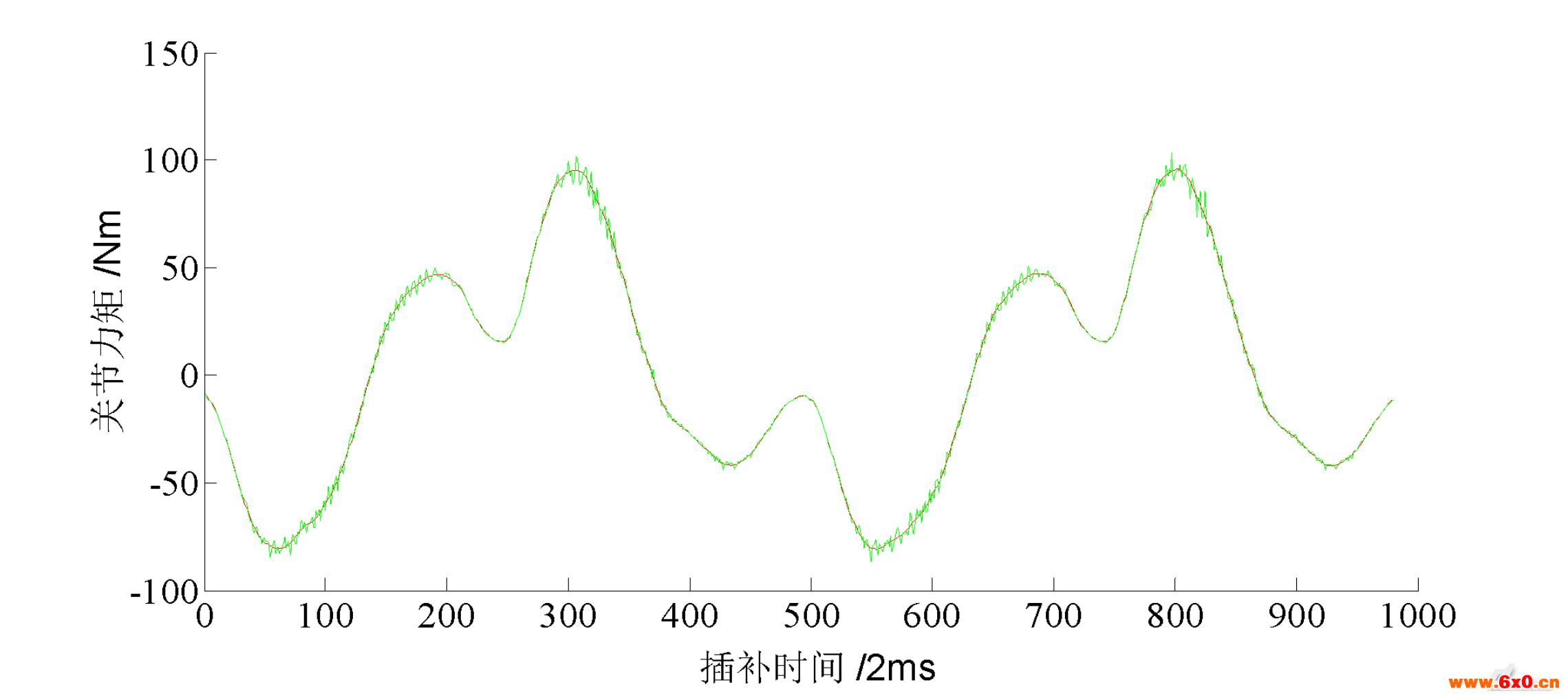
图5关节力矩的滤波效果图
Fig.5Thefilteringeffectofjointtorque

图6关节角加速度的滤波效果图
Fig.6Thefilteringeffectofjointangularacceleration
从图5和图6可以看出经过巴特沃斯低通滤波器进行滤波后,差分后的高频噪声和读到的力矩噪声,能很好地滤除,且没有相位偏移,这样可以在很大程度上保证参数辨识的精度。
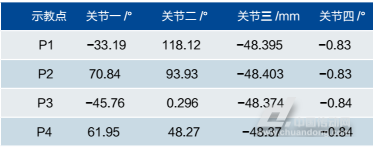
然后,在机器人的工作空间选取4个示教点(示教点的各关节转角见表1),分两组分别进行关节点到点运动。机器人的运动路径分别为P1到P2的点到点运动和P3到P4的点到点运动。为了加强实验对比,机器人运动时,分别使用基于惯性力模型的SCARA机器人加速度自适应控制方法(后文简称自适应控制)和传统的预先设定最大加速度的控制方法(后文简称传统控制)进行对比实验,设定关节一的极限力矩为70Nm,预先设定的速度、加速度和减速度值(速度单位为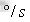 ,加速度单位为
,加速度单位为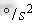 )如下图7所示:
)如下图7所示:

图7设定的各关节初始速度和加速度值
Fig.7Initialvelocityandaccelerationofeachsetofjoints
表1实验用示教点各关节转角
Tab.1thejointrotationanglesofteachingpoints

在循环运行P1到P2的点到点运动时,两种控制方法下的关节一关节力矩和关节角加速度的滤波后对比曲线图分别如图8(a)和8(b)所示:

图8(a)两种控制下关节一力矩对比图
Fig.8(a)Thecontrastofjointtorqueoftwokindsofcontrol

图8(b)两种控制下关节一角加速度对比图
Fig.8(b)Thecontrastofaccelerationofjointundertwocontrol
从图8(a)可以看出,在循环运行P1到P2的点到点运动时,使用自适应控制时,关节一的实际运行最大力矩控制在±70Nm左右,说明惯性力模型的精度可以达到要求,而使用传统控制时则为50Nm,自适应控制可以充分发挥电机的机械性能;同时,采用自适应控制时,关节的加速度和减速度根据起点和终点处的惯性项(M11,M12,M14)大小不同,呈现不对称分布,整体的运动节拍减小13.83%。
在循环运行P3到P4的点到点运动时,此时传统控制下,全速运行时机器人关节一电机因电流过大而报警,所以传统控制时按照85%倍率的运动学参数运行,两种控制方法下的关节一关节力矩和关节角加速度的滤波后对比曲线图分别如图9(a)和9(b)所示,同时也分析了两种控制情况下关节一电机轨迹跟踪误差曲线如图10所示:

图9(a)两种控制下关节一力矩对比图
Fig.9(a)Thecontrastofjointtorqueoftwokindsofcontrol

图9(b)两种控制下关节一角加速度对比图
Fig.9(b)Thecontrastofaccelerationofjointundertwocontrol

图10两种控制下关节一电机轨迹跟踪误差对比图
Fig.10Thecontrastoftrackingerrorofjointmotortrajectoryundertwocontrol
从图9(a)可以看出,在循环运行P3到P4的点到点运动时,使用自适应控制时,关节一的实际运行最大力矩控制在±70Nm左右,说明惯性力模型的精度可以达到要求,而使用传统控制时,因为加减速度不能自适应调整,起终点处的惯性力大小不同,造成起终点处的极限力矩分别为70Nm和-90Nm,终点处的实际驱动力矩已经超过极限力矩,使机器人抖动加大;而采用自适应控制时,关节的加速度和减速度根据起点和终点处的惯性力项大小不同(M11,M12,M14),呈现不对称分布。从图10可以看出,进行自适应控制时,关节一电机的轨迹跟踪误差有所减小,在路径终点附近最大减小19.76%,说明自适应控制时机器人运动的抖动较传统控制有一定程度的减小。
4总结
本文对基于惯性力模型的SCARA机器人加速度自适应控制进行研究。通过将带偏心负载的SCARA机器人简化成一个三连杆模型,根据机器人的实际特点,建立机器人的惯性力模型;采用中心差分和滤波的方法进行辨识数据的采集,辨识出各惯性项系数;建立基于惯性力模型的关节一角加速度自适应控制方法。最后,在开放式控制器的机器人平台上进行了自适应控制和传统控制的对比实验研究,实验结果表明,进行自适应控制时,能根据机器人位姿在插补开始之前,自适应调整关节一运行的最大角加速度,充分发挥机器人电机的机械性能,同时防止机器人因关节电机电流过大而报警,满足SCARA机器人高速高精度控制的要求。










 QQ交流群
QQ交流群

