非同轴两轮自平衡机器人是基于双陀螺转子的进动效应来实现自平衡。双陀螺转子的平衡作用可以加倍,但是其进动角过大与进动不同步是造成系统平衡失效的重要原因。针对前述问题,论文中提出了一种基于增益调度算法与进动角归零补偿的控制策略来消除进动角,同时采用机械方式来实现陀螺转子进动硬同步,可使系统倾斜角度与陀螺进动角度都逼近于零。论文中从系统的动力学建模、控制仿真、制作样机实验平台等方面进行了阐述,并开展了相关的实验来验证系统的平衡效果。实验结果表明,该系统具有很好的平衡性能和抗冲击能力,实时响应性高,稳态误差小,使非同轴两轮机器人走向应用更近一步。
两轮平衡机器人是载人移动机器人领域的研究热门,分为同轴两轮(左右布置)和非同轴两轮(前后布置)两种。同轴两轮机器人采用被动平衡方式,即需要依靠前后运动来实现动态平衡(类似倒立摆系统),已取得很多研究成果与应用,如大名鼎鼎的Segway。非同轴两轮机器人是一个欠驱动、非线性、侧向不稳定系统,其动力学与控制研究极具挑战性,目前仍处在实验室研发阶段。与同轴两轮机器人相比,非同轴两轮机器人的优点是动作灵活、良好的爬坡与越障能力、安全性好,有望用于载人交通工具、自主巡逻、侦查等领域。
1998年,俄罗斯莫斯科国立大学利用陀螺效应产生的进动力矩实现侧平衡,设计了一款具有自平衡功能的自行车。2005年,日本村田公司推出了会骑自行车的“村田男孩”,依靠安装在其胸部的一个垂直惯性轮实现左右平衡的。2011年,美国LIT汽车公司,申请了利用两个飞轮的陀螺效应来保持平衡的载人摩托车专利。2014年,美国俄亥俄州立大学以拉格朗日方程建立系统动力学方程,并设计一阶滑模控制器在自行车上开展了实验,具有较好的鲁棒性较。
然而,目前非同轴两轮机器人车仍面临的技术问题:平衡鲁棒性欠佳;抗撞击能力弱;高速行驶、小半径转向和爬坡等运动的稳定性不够。
论文介绍了一种可载人的非同轴两轮自平衡机器人,依靠一对陀螺转子同步进动产生的陀螺力矩来实现自平衡。该机器人是采用主动平衡方式,具有良好的平衡鲁棒性、抗冲击性以及调速性,可在静止或移动中实现平衡,故安全性更好。论文中从平衡原理、系统结构与动力学模型、控制系统方案、实验验证等方面进行了阐述。
原理与结构
单个陀螺转子进动产生的陀螺力矩τ,如图1所示,满足数学公式
 (1)
(1)
式中: 为陀螺转子的转动惯量;
为陀螺转子的转动惯量;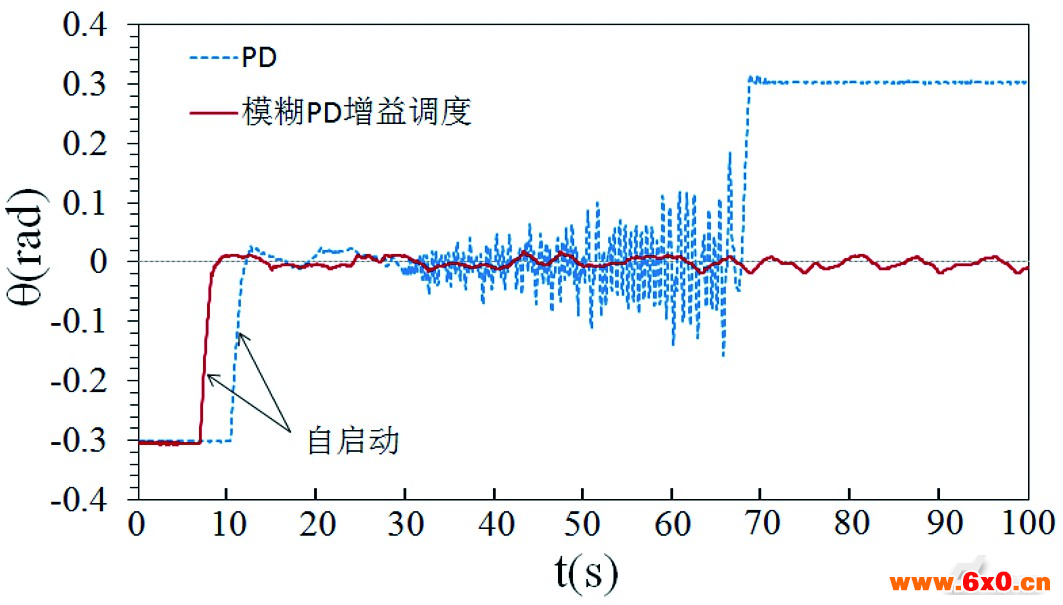 为陀螺转子自转角速度;
为陀螺转子自转角速度; 为陀螺转子进动角速度。陀螺力矩的方向符合右手定则,图中指向X轴负方向。陀螺力矩的方向是随进动角度变化而变化的。
为陀螺转子进动角速度。陀螺力矩的方向符合右手定则,图中指向X轴负方向。陀螺力矩的方向是随进动角度变化而变化的。
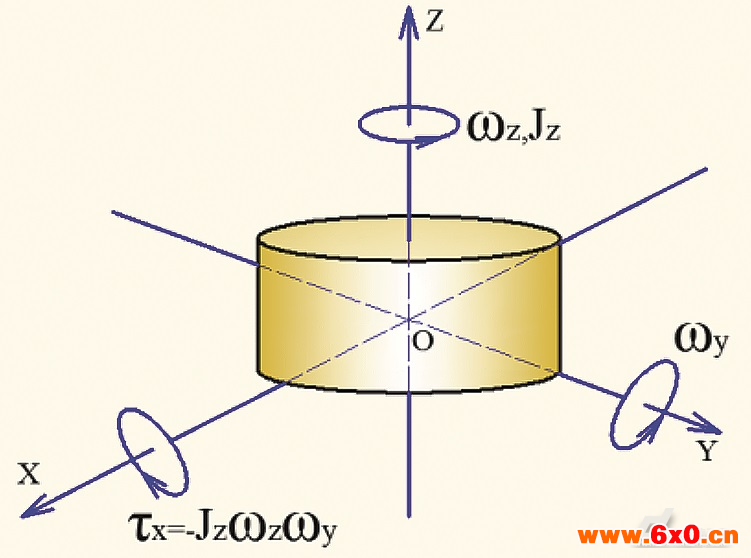
图1 陀螺转子陀螺效应原理图
由于进动角的存在,陀螺力矩会分解成翻滚力矩和航向力矩,前者是起平衡作用的有效力矩,而后者则是影响平衡稳定的干扰力矩,因此单陀螺平衡效果很差。论文中采用的双陀螺平衡的结构示意图如图2所示。为了使两陀螺转子的翻滚力矩是作用叠加而航向力矩是相互抵消,应采用保证两陀螺转子的自转方向和进动方向都相反。
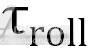
图2 陀螺装置平衡机理分析图
据图2所示,车身机体坐标系X1Y1Z1、陀螺转子坐标系X2Y2Z2和陀螺转子坐标系X3Y3Z3这三个坐标系处于同一平面内(即Y1、Y2、Y3轴的方向相同,由纸面朝外),其中X1轴为车身前进方向。为了便于分析,令两个陀螺的进动角速度大小相等、方向相反。假设某刻两陀螺的进动角度为,则双陀螺转子进动过程中在X1轴方向产生的翻滚力矩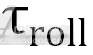 ,满足数学公式
,满足数学公式
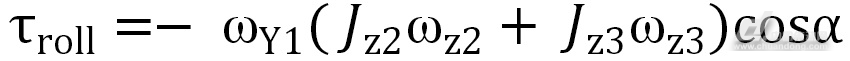 (2)
(2)
式中: 2、
2、 3为陀螺转子的转动惯量;
3为陀螺转子的转动惯量; 2、
2、 3为陀螺转子自转角速度;
3为陀螺转子自转角速度; 1为陀螺转子进动角速度。翻滚力矩方向X1轴负方向。
1为陀螺转子进动角速度。翻滚力矩方向X1轴负方向。
而两个陀螺在Z1轴方向产生的航向力矩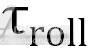 ,满足数学公式
,满足数学公式
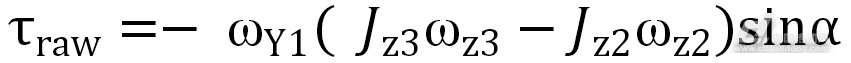 (3)
(3)
由上式可知,当两陀螺结构参数一致且进动速度大小相同时,航向力矩为零,所以双陀螺装置的优势在于可以抵消因单陀螺进动而产生的干扰力矩,使系统实现平衡稳定。为了保证两陀螺转子进动过程的同步性,论文中平衡装置采用机械方式来实现同步运动,即用同步带传动机构。由此可知,进动角速度与进动角度是控制系统平衡的关键因素。
为进一步简化分析过程,假设机器人的前、后轮与地面的接触点都落在地理坐标系XYZ的X轴上,且机体坐标X1与地理坐标X轴平行,其动力学模型为如图3所示。在忽略空气阻力、轮胎与地面之间力矩的前提下,当车身相对于Z轴的倾斜角为θ时,可得到平衡车动力学方程为
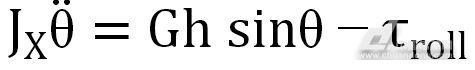 (4)
(4)
式中: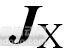 为车身相对于X轴的转动惯量;
为车身相对于X轴的转动惯量;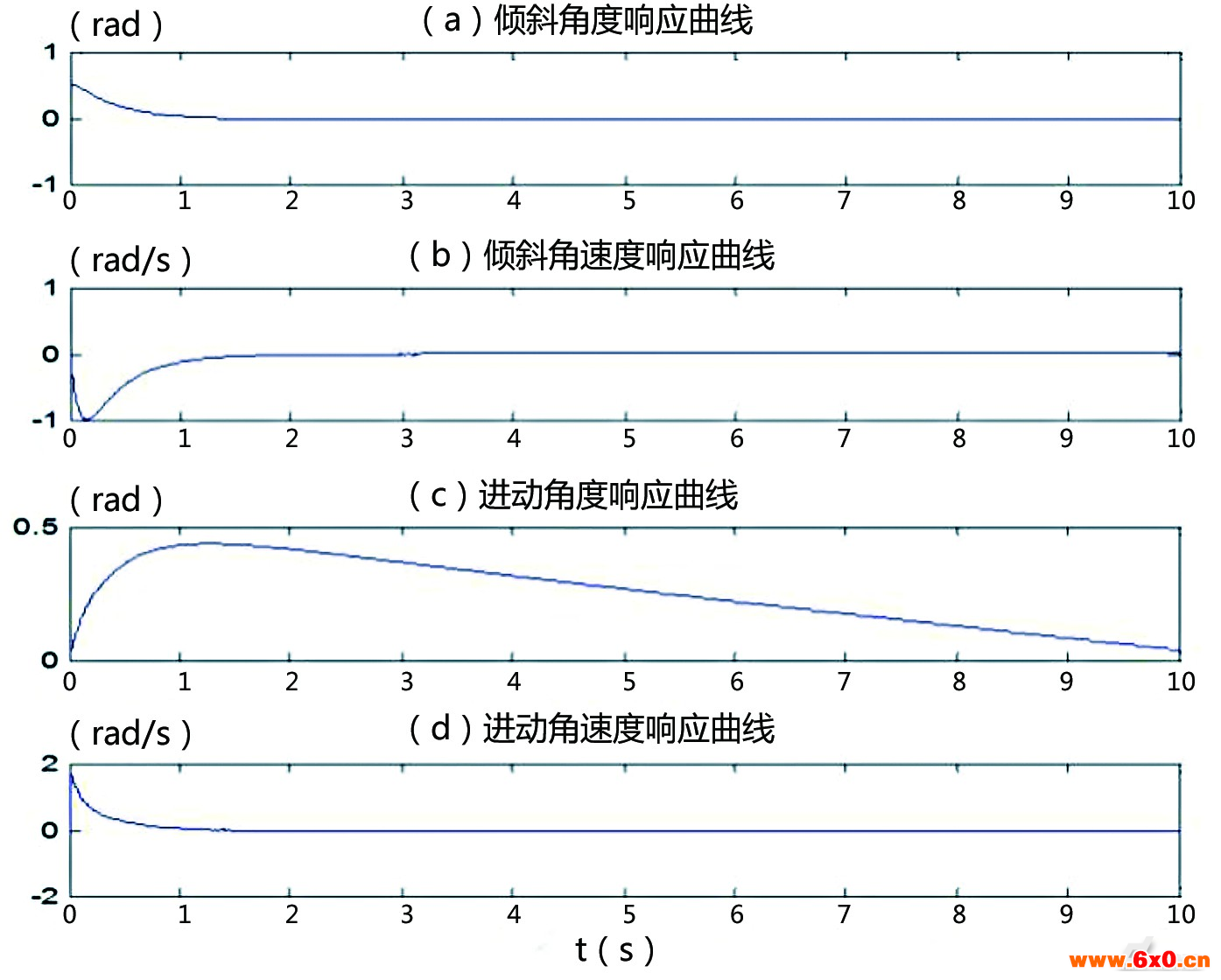 为车身左右倾斜的角加速度(即翻滚角加速度);G为机器人所受重力;h为重心与O点的距离。
为车身左右倾斜的角加速度(即翻滚角加速度);G为机器人所受重力;h为重心与O点的距离。
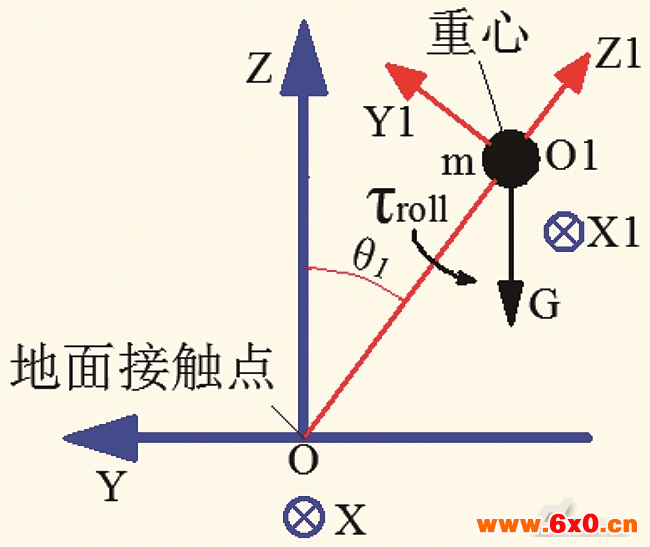
图3 系统简化力学模型
非同轴两轮自平衡机器人的机械结构实物如图4所示,其整体结构由三部分组成:车头、车尾、车身。车头部分包括橡胶轮、舵机与前轮转向机构等;车尾部分主要轮毂电机、减震机构等;车身包括双陀螺平衡装置与电控系统。双陀螺平衡装置由前后陀螺转子、无刷电机、陀螺转子同步机构、陀螺进动电机等构成。电控系统由主控制板、电机驱动器及传感器、锂电池组等构成。

图4 非同轴两轮自平衡机器人
平衡控制方案
非同轴两轮自平衡机器人的控制系统硬件组成如图5所示。控制系统按功能分为五个单元:上位机、主控单元、驱动器、传感器检测和电源管理。电机包括四种类型:陀螺自转电机、陀螺进动电机、前轮转向舵机、后轮前进驱动电机。
图5 控制系统硬件组成
自平衡机器人系统最重要的参数是车身倾斜角度θ,要实现平衡应使θ为零。单纯的PD控制可以使车身实现短暂的平衡,但无法持续稳定,系统容易震荡直至奔溃。究其原因,自平衡机器人是一个非线性、耦合的系统,而且为了抵抗车身外力矩(主要是重力矩)的存在,陀螺会始终朝一个方向进动,从而导致进动角过大,陀螺效应的平衡作用失效。
在平衡控制过程中,系统需要加入一个陀螺进动角归零补偿量θα使陀螺进动角度趋向于零,否则车身会因陀螺效应失效而倾倒。论文中采用了模糊PD与增益调度来控制机器人的自平衡过程,如图6所示。平衡控制器通过增益调度来减小车身左右震荡,而这些参数值都由实验测试得到。

图6 非同轴两轮机器人的平衡控制方块图
由日常经验可知,以一定速度来驾驶自行车或摩托车转弯时,车身需要倾斜一定角度才能保证转弯不倒,这是因为转弯过程中需要车身提供一个向心力。考虑到转弯因素,车身的左右动力学方程就由(4)变成
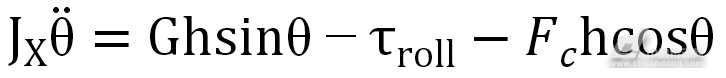 (5)
(5)
式中:FC为车身转弯时产生的离心力。
而转弯时,车身倾斜角度θ与转弯角度β之间的关系
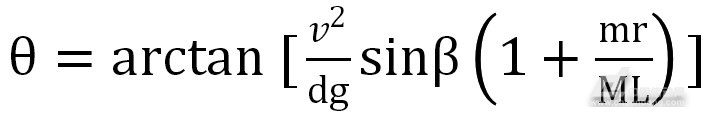 (6)
(6)
式中:v为车身前进速度;d为前后轮胎着地点之间的距离;g为重力加速度;m为车身质量;M为总质量(加上负载);L为车身重心高度。
为解决转弯时平衡问题,PD控制中还需要加入一个基于转弯离心力的倾角补偿量 (其大小与前轮转弯角度和后轮转速相关)。
(其大小与前轮转弯角度和后轮转速相关)。
车身倾斜角度的总补偿量为 ,从而得到车身倾斜角偏差为
,从而得到车身倾斜角偏差为
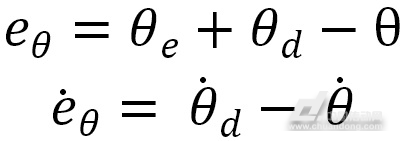 (7)
(7)
式中:为期望的倾斜角;为倾斜角总补偿量。
那么通过模糊PD控制器来控制前后两个陀螺产生的翻滚力矩为
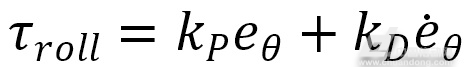 (8)
(8)
式中: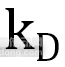 为前后陀螺转子产生的总翻滚力矩;
为前后陀螺转子产生的总翻滚力矩; 和
和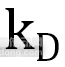 为模糊PD控制器输出控制增益。
为模糊PD控制器输出控制增益。
根据模糊理论取倾斜角度和倾斜角速度的模糊子集为{NB,NM,NS,Z,PS,PM,PB}。根据模糊子集和自平衡机器人系统的动力学简化模型,模糊输入参数倾斜角度误差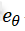 与角速度误差
与角速度误差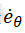 的模糊论域为[-1,1],量化等级为{-1,0.5,-0.25,0,0.25,0.5,1},量化因子分别为0.3rad和1rad/s。模糊输出控制量的论域[-1,1],量化等级为{-1,0.5,-0.25,0,0.25,0.5,1},比例因子为10rad/s。输入与输出隶属的函数如图7所示。
的模糊论域为[-1,1],量化等级为{-1,0.5,-0.25,0,0.25,0.5,1},量化因子分别为0.3rad和1rad/s。模糊输出控制量的论域[-1,1],量化等级为{-1,0.5,-0.25,0,0.25,0.5,1},比例因子为10rad/s。输入与输出隶属的函数如图7所示。
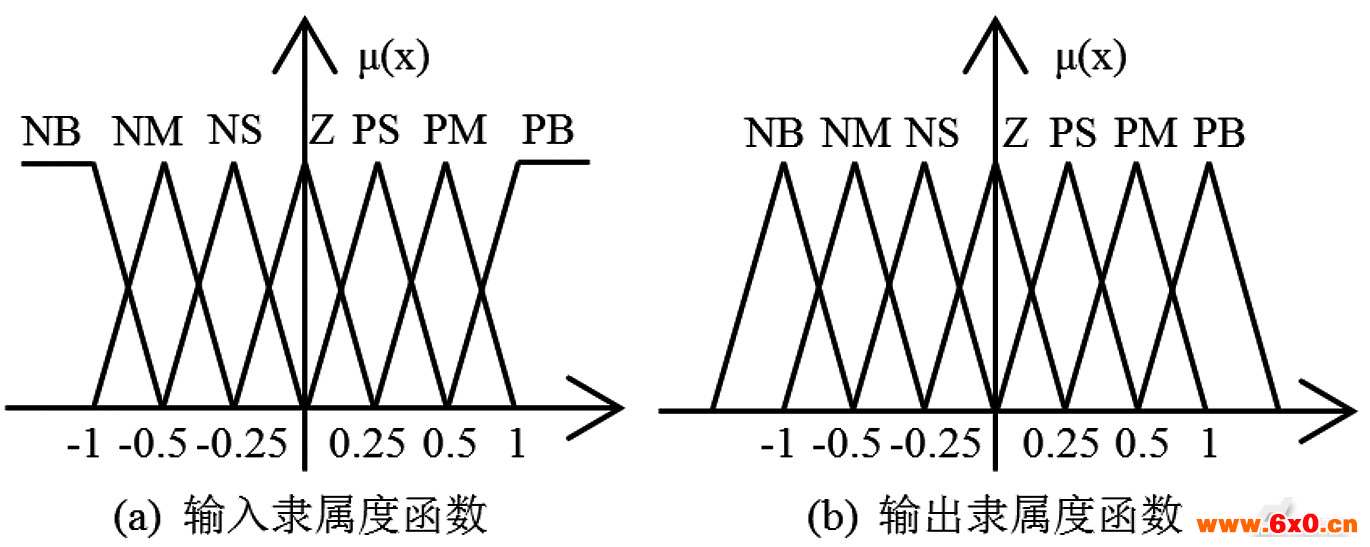
图7 输入输出隶属度函数
而模糊控制规则见表1所示。
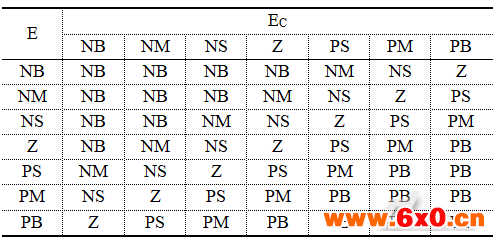
表1模糊控制规则表
通过MATLAB仿真得到平衡机器人的动态数据时间响应曲线如图8所示,由仿真结果可以看出系统能快速进入平衡稳定状态。

图8 车身自平衡过程中姿态参数响应曲线图
实验与结果分析
文中针对非同轴两轮机器人的平衡性能开展了一些实验验证,分别采用PD和模糊PD增益调度方式在样机上进行了对比测试。实验样机的具体规格参数如表2所示,主控单元芯片采用ARM,数据采样率为100Hz。
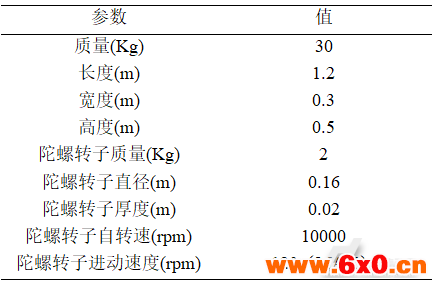
表2 系统规格参数
从静止倾斜倒地至自动恢复平衡过程中,车身的倾斜角度与角速度变化曲线如图9所示。由图可知,车身刚开始处于左侧倾倒状态,由倾倒状态变成平衡状态只需要1~2s内就可以完成。单纯采用PD控制方式只能维持车身在平衡状态附近十几秒,然后很快出现高频震荡直至系统奔溃倾倒在右侧。而模糊PD增益调度控制方式能始终维持车身在平衡状态,超调量小且稳定状态下车身倾斜角度θ处在-0.02rad~+0.02rad之间(即偏差小于1.5°)。

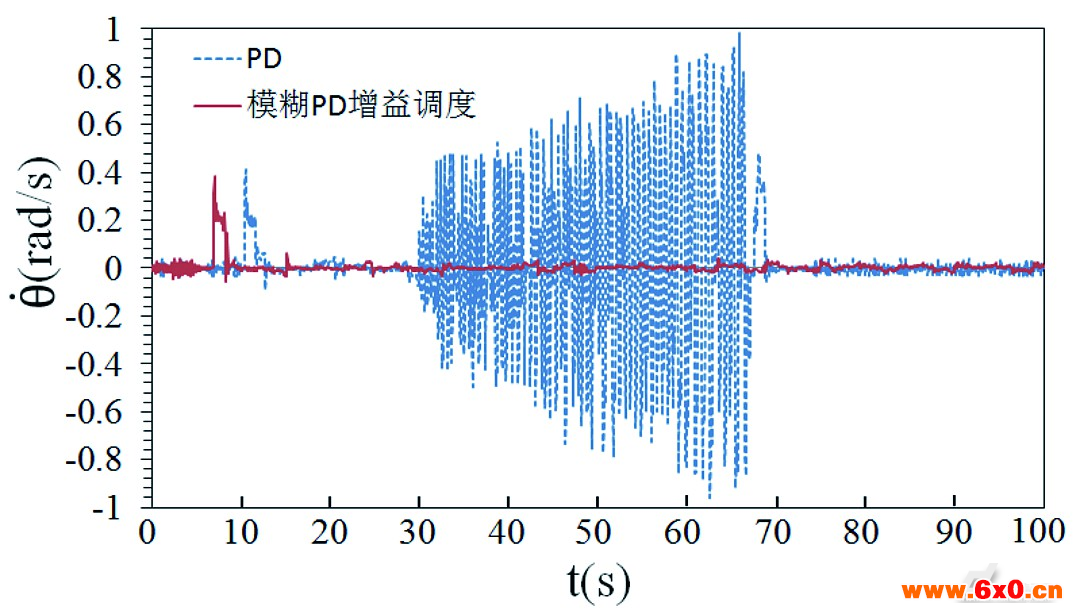
图9 车身自平衡过程中倾斜角度与角速度
在车身自平衡过程中,陀螺的进动角与角速度的变化曲线如图10所示。同样地可以看出,当采用纯PD控制方式时,陀螺转子进动角度在30s时刻开始高频震荡直至陀螺力矩失效状态。而当采用模糊PD增益调度方式时,陀螺进动角终态偏差处于-0.2rad~-0.1rad之间。从图中可以看出,陀螺进动角度终态的偏差中心并未处于0线上,是由于制作的样机重心偏向右侧形成偏心力矩所致,陀螺需要不断地朝一个方向进动来产生抵抗力矩。
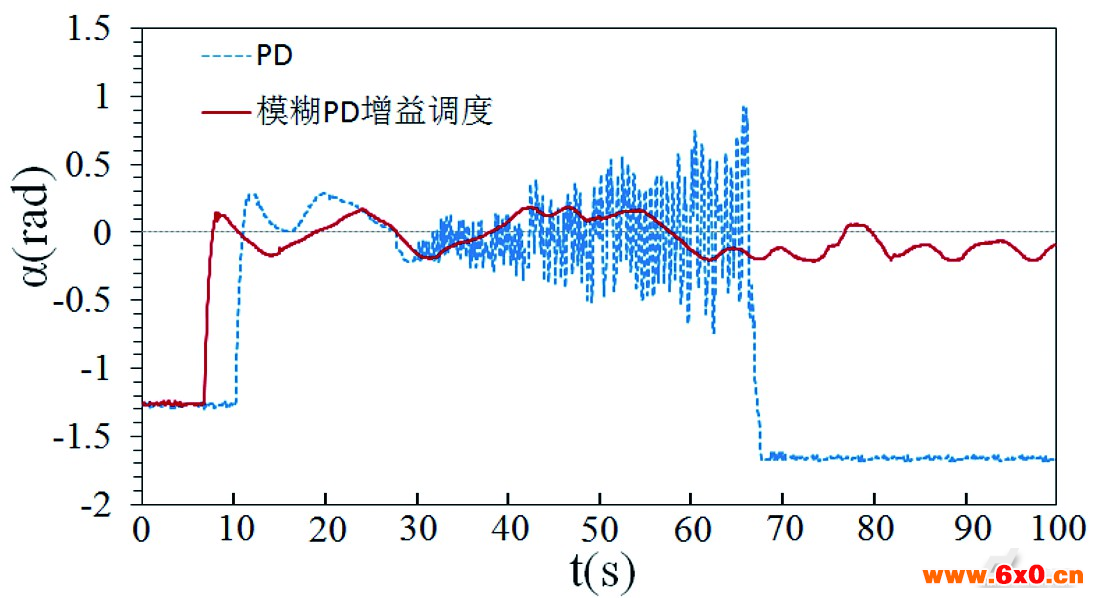
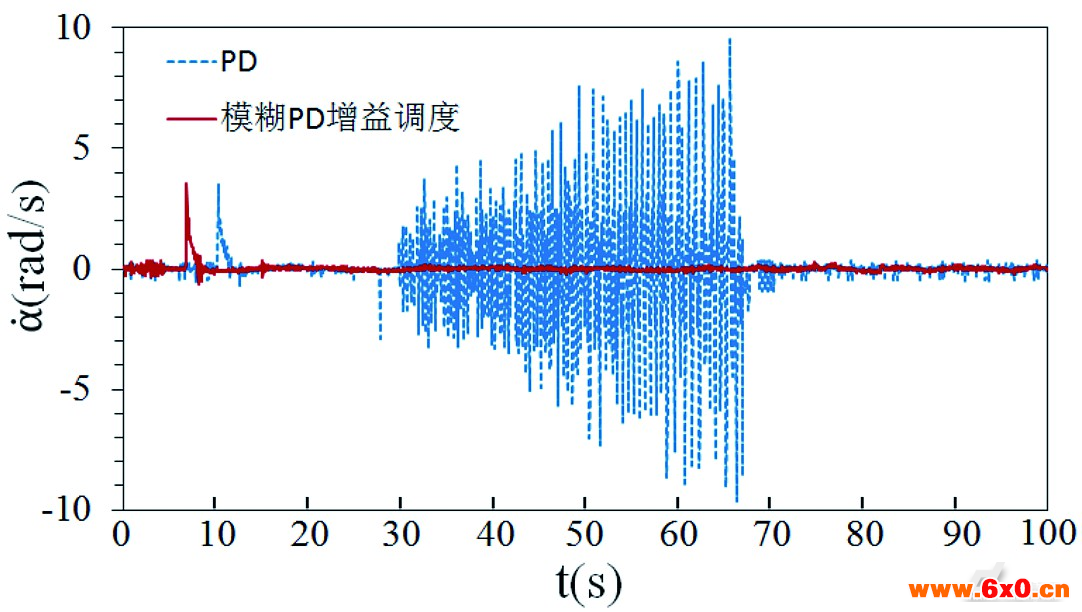
图10 陀螺进动角度与角速度
结语
论文中开发的非同轴两轮的载人交通工具原理样机能够实现自动平衡。由实验结果可知,非同轴两轮自平衡机器人采用纯PD控制平衡的效果不太理想,而采用模糊PD增益调度方式的平衡性能则表现很好,车身倾斜角与陀螺进动角度都处在一个比较稳定、合理的范围内。










 QQ交流群
QQ交流群

