摘要:由于机械加工误差、装配误差与间隙,摩擦磨损等因素的影响,SCARA机器人的实际臂长与理论臂长存在一定偏差;通常难以保证机器人大小臂严格成一直线,造成零点偏移。实际零点及臂长与理论值的偏差,影响机器人的绝对定位精度。传统的标定方法需要昂贵的测量设备,标定过程复杂,不利于现场标定。本文提出一种实用、简单、高效的SCARA机器人零点及臂长标定方法。机器人末端标定针分别以左右手系对准已知距离的两标定孔,即可完成标定。仿真及实验结果表明,该方法稳定,精度较高,标定后机器人的左右手系定位精度在0.09mm以内。
1 引言
1978年,日本山梨大学牧野洋发明SCARA(SelectiveComplianceAssemblyRobotArm),该机器人具有四个轴和四个运动自由度(包括沿X,Y,Z方向的平移和绕Z轴的旋转自由度),如图1。SCARA机器人在X,Y方向上具有顺从性,而在Z轴方向具有良好的刚度,此特性特别适合于装配工作;其串接的两杆结构,类似人的手臂,可以伸进有限空间中作业然后收回,适合于搬动和取放物件。SCARA机器人结构紧凑、动作灵活,速度快、位置精度高,广泛应用于电子产品工业、药品工业和食品工业等领域。
由于机械加工误差、装配误差与间隙,摩擦磨损等因素的影响,实际机器人的运动学参数(如臂长,减速比等)与理论设计值存在一定偏差;SCARA机器人大臂与小臂成一直线的位置为其零点位置,通常难以保证大小臂严格成一直线,造成零点偏移。实际的零点及臂长与理论值的偏差,会影响机器人的绝对定位精度。
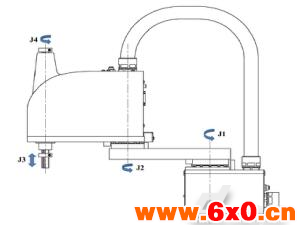
图1 SCARA机器人
Fig.1 SCAR Arobot
文献[1]提出单基准点校正和三基准点校正两种方法对平面二自由度机器人进行标定,但只对关节误差进行校正,没有对臂长进行标定。文献[2]提出了一种通用的串联机器人标定方法,实验结果表明,该方法大大提高了机器人的绝对定位精度,但必须借助高精度的测量设备。文献[3]提出了基于单点约束的标定方法,但是有些参数必须依靠测量设备获得。文献[4]提出了一种现场应用中无需测量设备的单点两步标定法,但其中必须求解非线性优化问题,实现起来较复杂。文献[5]提出了基于SVD分解的四孔标定板标定方法,该方法简单实用,精度较高,但是对标定板四个孔的机械加工精度要求较高。
本文提出了一种简单、实用的SCARA机器人零点及臂长标定方法。该方法无需专门测量设备,标定过程极其简单,能够方便且准确标定出SCARA机器人的零点与臂长。
2 零点及臂长标定原理
由于SCARA机器人的零点与臂长标定与三、四轴没有关系,本文将SCARA机器人视为平面二自由度机器人。
2.1 SCARA机器人运动学正解

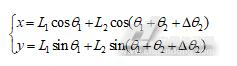 (1)
(1)
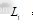
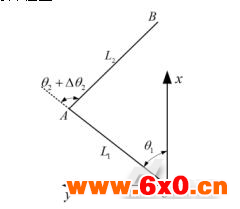
图2 SCARA机器人运动学正解示意图
Fig.2 Schematic diagram of SCARA forward kinematics
2.2零点及臂长标定步骤

图3臂长与零点标定示意图
Fig.3 Schematic diagram of arm length and zero position calibration
2.3零点及臂长标定原理推导
机器人末端标定针分别以不同手系对准孔M,根据式(1),可以得到方程组:
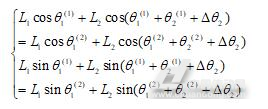 (2)
(2)
利用三角恒等式:
 (3)
(3)
并做变量代换:
 (4)
(4)
为简化符号,记:
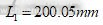 (5)
(5)
式(2)可以写成:
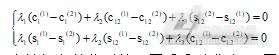 (6)
(6)
末端标定针分别以不同手系对准孔N,同理可以得到方程组:
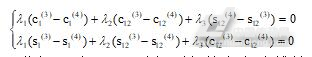 (7)
(7)
联立(6)和(7)可以得到超静定齐次线性方程组,可以利用最小二乘法求解。对于任意非零实数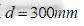 ,齐次线性方程
,齐次线性方程
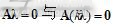 同解,不失一般性,可以加入约束
同解,不失一般性,可以加入约束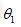 。求解超静定齐次线性方程组的问题可以转化为带等式约束的优化问题:
。求解超静定齐次线性方程组的问题可以转化为带等式约束的优化问题:
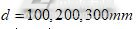 (8)
(8)
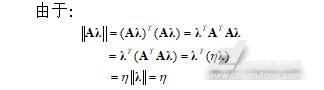 (9)
(9)
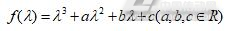 (10)
(10)

根据式(4),可得零点偏移值:
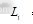 (11)
(11)
大臂与小臂长度的比例值:
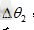 (12)
(12)
由于孔M与孔N的长度d已知,利用式(1),可以求臂长实际值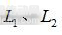 。
。
 (13)
(13)
同理可得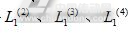 ,大小臂长度:
,大小臂长度:
 (14)
(14)
3 算法稳定性分析
由SCARA机器人的运动学正解可以看出,影响绝对定位精度的因素有:大臂长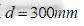 、小臂长
、小臂长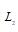 、零点偏移值
、零点偏移值
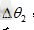 ,关节1角度
,关节1角度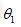 ,关节2角度
,关节2角度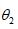 。由于关节1和2的角度由编码器读数与减速比确定,通常编码器与减速机精度都很高,在此认为关节角度是准确的。因此,对于本文提出的标定算法,影响机器人零点及臂长标定精度有两方面:末端标定针对点的精度与标定板孔距。
。由于关节1和2的角度由编码器读数与减速比确定,通常编码器与减速机精度都很高,在此认为关节角度是准确的。因此,对于本文提出的标定算法,影响机器人零点及臂长标定精度有两方面:末端标定针对点的精度与标定板孔距。
设SCARA臂长与零点理论值为: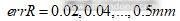 ,
, 。臂长与零点实际值为:
。臂长与零点实际值为: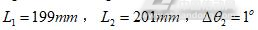 。分别取标定板孔距
。分别取标定板孔距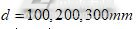 ,标定针对点误差为以准确点为圆心,误差半径为
,标定针对点误差为以准确点为圆心,误差半径为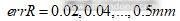 的误差圆。利用MATLAB随机模拟标定过程10000次,可以求得在不同的标定板孔距与对点精度下的标定结果,进而求得大小臂长度和零点偏移值的标准差,仿真结果如图4~6。
的误差圆。利用MATLAB随机模拟标定过程10000次,可以求得在不同的标定板孔距与对点精度下的标定结果,进而求得大小臂长度和零点偏移值的标准差,仿真结果如图4~6。
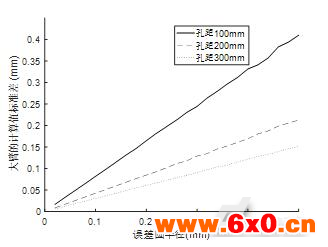
图4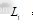 的计算值标准差与孔距、误差圆半径的关系
的计算值标准差与孔距、误差圆半径的关系
Fig.4 The relation between standard deviation of calculated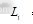 and hole distance and error radius
and hole distance and error radius
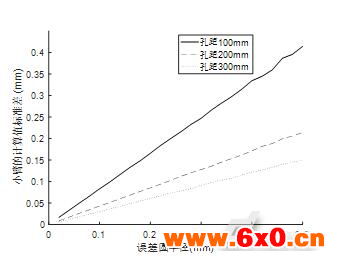
图5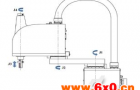 的计算值标准差与孔距、误差圆半径的关系
的计算值标准差与孔距、误差圆半径的关系
Fig.5 The relation between standard deviation of calculated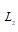 and hole distance and error radius
and hole distance and error radius
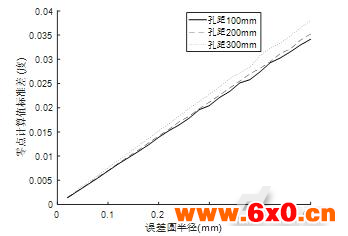
图6 的计算值标准差与孔距、误差圆半径的关系
的计算值标准差与孔距、误差圆半径的关系
Fig.6 The relation between standard deviation of calculated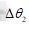 and hole distance and error radius
and hole distance and error radius
由图4~6可以得出:本文提出的SCARA机器人零点及臂长标定算法稳定。孔距越大,臂长的计算值的稳定性对对点误差的抗干扰能力越强。零点偏移值的计算值的稳定性很好,不同孔距对偏移值的计算值的稳定性影响小。
4 标定实验
本文采用深圳众为兴技术股份有限公司(下文简称“众为兴”)自主研发的AR4215SCARA机器人进行实验。如图7为末端带标定针的AR4215机器人。机器人大臂设计值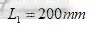 ,小臂设计值
,小臂设计值 ,标定板孔距
,标定板孔距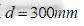 。标定板在机器人工作空间平面里随意摆放,根据标定步骤进行实验,采用机器人的轻松拖拽功能,可以很方便完成实验。测量数据及标定结果如表1。取5次标定结果的平均值,计算得到实际大臂长度
。标定板在机器人工作空间平面里随意摆放,根据标定步骤进行实验,采用机器人的轻松拖拽功能,可以很方便完成实验。测量数据及标定结果如表1。取5次标定结果的平均值,计算得到实际大臂长度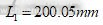
,小臂长度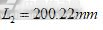 ,零点偏移值
,零点偏移值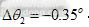 。
。

图7 AR4215 SCARA 机器人
Fig.7 AR4215 SCARA robot
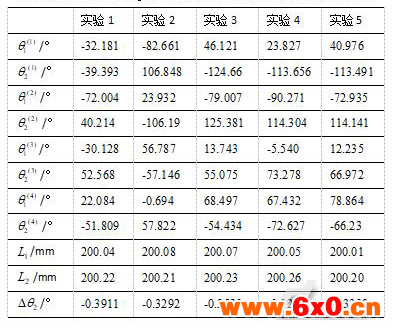
表1 标定实验数据及计算结果
Tab.1 Calibration experimental data and calculation results
5 标定验证
本文采用众为兴自主研发的AVS视觉系统及大恒CCD工业相机,分辨率1628*1236。标定验证的实验平台,如图8。

图8 标定验证实验平台
Fig.8 Experiment platform for calibration verification
5.1 求平均像素当量

5.2 左右手系定位精度验证
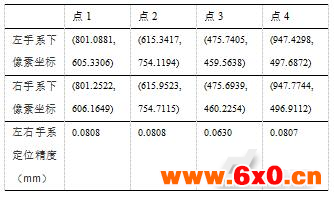
以SCARA机器人末端丝杆内圆为模板,在相机视野里随机选取4个验证点,机器人分别以左右手系运动到这些点,并用AVS视觉系统得出丝杆内圆圆心的像素坐标。测量及计算结果如表2。
表2 标定实验数据及计算结果
Tab.2 Calibration experimental data and calculation results
6 结论
本文提出一种实用、简单、高效的SCARA机器人零点及臂长标定方法。只需拖拽机器人末端标定针分别以左右手系对准已知距离的两标定孔,记录当前关节1和关节2的角度,即可完成标定,操作步骤极其简单。标定孔只需满足距离精度要求,大大降低标定板的机械加工难度。相对于传统的标定方法需要昂贵的测量设备,标定过程复杂的特点,该方法更有利于SCARA机器人现场标定。仿真结果表明,该标定方法稳定,且孔距越大,臂长的标定结果越稳定,零点的标定结果受孔距的影响小。实验结果表明,该标定方法精度较高,标定后,机器人同一个点的左右手系定位精度在0.09mm以内。










 QQ交流群
QQ交流群

