推杆减速器的效率计算与强度校核
推杆减速器的啮合效率是衡量其性能的一个重要指标,而强度校核是确定其承载能力的主要依据。对它们的理论分析能否正确反应推杆减速器的实际情况,直接影响到推杆减速器优化设计的效果。
推杆减速器由于采用推杆这一特殊构件作为活齿,因而使得它在效率与强度计算方法上与其它活齿传动机构有所不同。其特点是传动圈导槽对推杆等效全反力的作用点及方向随推杆工作位置的不同而发生的变化很大。因而与其它活齿传动机构(例如滚柱活齿减速器)的效率计算方法是不同的。在已发表的有关推杆减速器效率计算的文献中,都近似地把在外滚子与内齿圈之间作用力固定不变的情况下,无摩擦损失时与有摩擦损失时所需的驱动力或驱动力矩的比值作为啮合效率。有的虽然考虑了驱动力矩,但同时又把有摩擦时的驱动力近似处理为通过内滚子中心。实际计算表明,这些近似处理方法所带来的误差是很大的。而且这些文献只讨论了单个推杆的啮合效率。
本章详细分析了推杆在不同情况下的受力状态,考虑了惯性力的影响,严格按啮合效率定义推导出了较为精确的总体啮合效率计算公式,并利用计算机能够进行大量复杂运算的特点,取机构在若干不同啮合点位置时效率的平均值作为总的啮合效率,计算结果与实验数据基本相吻合。
3.1推杆在导槽内的运动分析
在推杆减速器中,动力的传递是靠运动着的推杆来完成的,推杆在工作行程中相对导槽的运动是变速的外推滑动,其速度ur可用内滚子中心01点的速度表示,如图2.7所示。在前面已求得当传动圈固定时,内滚子中心Ol点的位移为:
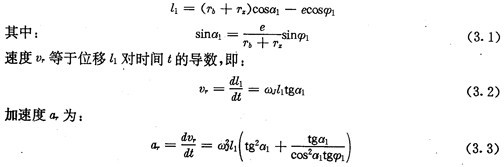
推杆在工作行程开始时,ι1值为最小,这时ιmin=Tb+Te-e,a1=0,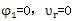 ,
,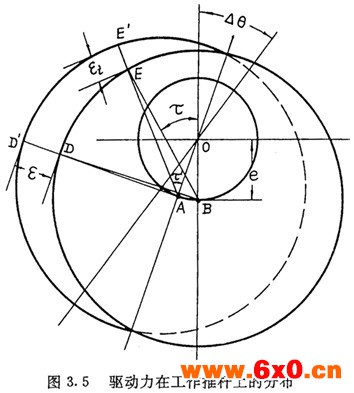 加速度方向同运动方向一致,即从内向外作加速运动。
加速度方向同运动方向一致,即从内向外作加速运动。
推杆在工作行程结束位置,ι1达到最大值ιmin=Tb+Tz+e,此时a1=0,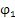 =π,
=π,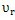 =0,
=0,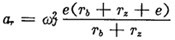 加速度方向与运动方向相反,即作减速运动。
加速度方向与运动方向相反,即作减速运动。
为求出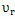 ,命ar=0,可得:
,命ar=0,可得:
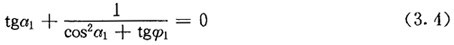
联立(3.4)式及(3.1)式,可求得ar=0时对应的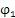 值,由此可得到该位置各运动参数的值,此时速度有最大值urmax。
值,由此可得到该位置各运动参数的值,此时速度有最大值urmax。
[算例]
对于3TWY7.5-12推植减速器,Tb=55mm,Tz=10mm,ε=5mm,ι=36mm,ωJ=1500RPM,iJN=-11,计算出的ι1, ,ar与
,ar与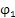 的关系曲线如图3.1所示。
的关系曲线如图3.1所示。
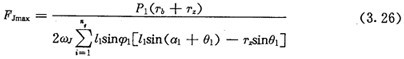
3.2推杆受力分析
在第二章已把推杆减速器根据传动圈是否与激波器转向相同分为正反两种结构。这两种结构的受力状态是不同的。下面先讨论正向结构。
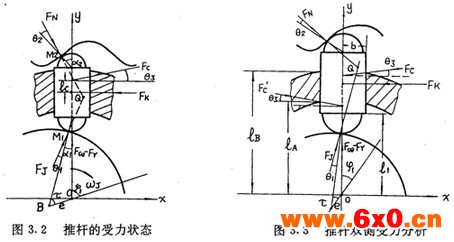
设激波器按顺时针方向转动,如图3.2所示,则激波器迫使与其接触的内滚子自身以逆时针方向转动,在激波器与内滚子接触点M1处,激波器转动的弧长大于内滚子转动的弧长,所以激波器对内滚子的摩擦力方向是沿切线方向向右,与激波器沿接触点法线方向对内滚子的作用力一起组成全反作用力FJ。在外滚子与内齿圈接触点风处,外滚子沿齿廓向齿根方向运动,内齿圈齿廓对外滚子的摩擦力方向为沿齿廓指向齿顶的切线方向,与内齿圈沿接触点M2法线方向对外滚子的作用力一起组成全反力FN。
在传动圈导槽与推杆的接触处,受到传动圈导槽对推杆的向下摩擦力,与沿法线方向的约束反力一起组成全反力FC。
图3.2中的θ1、θ2 、θ3分别为激波器与内滚子之间、内齿圈齿廓与外滚子之间以及导槽与推杆之间的摩擦角。
如上节所述,催件在随传圈作匀速运动的同时,还相对导槽作加速度为ar的加速运动。根据达朗伯原理,除了上述真实的作用力及约束反力外,再假想地加上惯性力的反力,这些力在形式上组成一个平衡力系。推杆所产生的惯性力由三部分组成:向心力Fω,相对惯性力Fr,科氏惯性力Fk,它们的作用点可看作是推杆的质心,其反力的方向如图3.2所示,由理论力学知,它们的计算按下式:
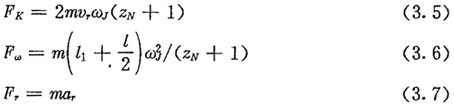
式中m是推杆的质量。
3.2.1推杆单侧受力的平衡方程
当FJ、FN二力的交点Q落在传动圈所在环内(图3.2所示),推杆呈现单侧受力状态(右侧受力),对推杆质心取矩,可得如下平衡方程式:
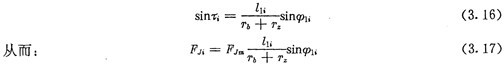
由于考虑了惯性力,所以力Fc 不通过交点Q,lc也是一个未知数。若根据输入功率确定出FJ,则方程组(3.8)只剩下FN、FC及lc三个未知数了。
3.2.2推杆双侧受力的平衡方程
若传动圈尺寸选用不当,或者是机构为反向结构,使FJ与FN作用力的交点Q 落在传动圈所在环外(图3.3所示)时,推杆呈现双侧受力状态。生产实践表明,推杆双侧受力将造成推杆严重的磨损。这种情况下推杆的受力与传动圈外径尺寸有关。对于图3.3所示受力情况,对推杆质心取矩,可列出它的平衡方程式为:
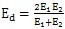
3.2.3反向结构的受力分析
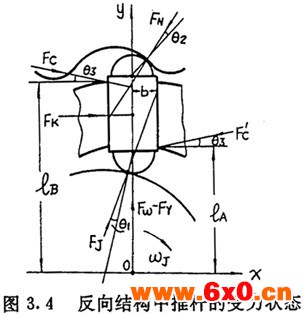
在传动圈与激波器转向相反的结构中,工作推杆的受力状诚如图3.4所示。从受力状态图可以看出,在运动过程中,推杆与导槽必然形成双侧接触。推杆两侧将造成严重磨损,实际生产中,应避免使用反向结构。
3.3效率计算
3.3.1单个推杆的效率计算
从方程组(3.8)中消去FN得:

3.3.2整体效率计算
从上面单个推杆的效率计算公式可知,对应激波器的不同转角,效率是不同的。实际上总有多个推杆同时工作,因而应求出整个机构的总体效率。
下面首先来分析驱动力在工作推杆上的分布规律。
设传动构件之间无间隙,并设激波器是完全刚性的。在驱动力矩作用下,各工作推杆的内滚子在与激波器接触处产生法向弹性变形,使激波器转过一个微小的角度△θ,如图3.5所示,则可确定弹性变形量εi的分布规律。

设最大弹性变形量为ε,由图3.5可知:


上式中:FJm为对应最大变形处的作用力;FJi为激波器对第i个推杆的作用力;τi为第i个推杆内滚子中心与激波器短轴所夹的圆心角。如图3.2所示。
在任 一瞬间,各工作推杆所处的位置是不同的,设第i个工作推杆所对应的激波器转角为,则:
一瞬间,各工作推杆所处的位置是不同的,设第i个工作推杆所对应的激波器转角为,则:
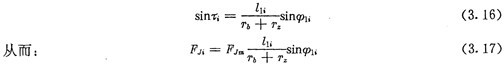
由于相邻两推杆所夹的中心角为2π/ZC,在某一时刻,只要其中 一个工作推杆所对应的激波器位置角(激波器相对该推杆从初始工作位置转过的角度)确定后,其它各工作推杆所对应的激波器位置角也随之确定下来。设各工作推杆所对应的最小激波器位置角为
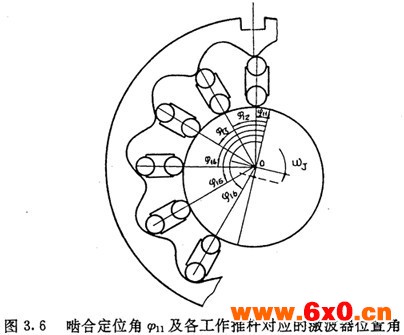
一个工作推杆所对应的激波器位置角(激波器相对该推杆从初始工作位置转过的角度)确定后,其它各工作推杆所对应的激波器位置角也随之确定下来。设各工作推杆所对应的最小激波器位置角为 ,如图3.6所示,则从对应激波器位置角为
,如图3.6所示,则从对应激波器位置角为 的这个工作推杆开始,顺序第i个工作椎杆所应的激波器位置角为
的这个工作推杆开始,顺序第i个工作椎杆所应的激波器位置角为 :
:

这样,一旦最小激波器位置角 被确定,各工作推杆所对应的激波器位置角
被确定,各工作推杆所对应的激波器位置角 便随之被确定下来,从而各啮合点也被确定下来,称最小激波器位置角
便随之被确定下来,从而各啮合点也被确定下来,称最小激波器位置角 为啮合点定位角,简称啮合定位角。啮合定位角
为啮合点定位角,简称啮合定位角。啮合定位角 的取值范围是:
的取值范围是:
0≤ <
<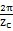
类似方程组(3.8)的建立及求解,可得第i个工作推杆的Fci及lci,与式(3.10)及(3.11)类同。
考虑到实际装置为双排结构,输入功率P1可表示为:
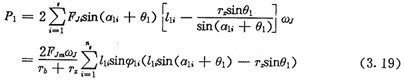
为使表达式简洁,本文下面在累加符号“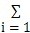 ”后的式子中,各参量对应的下标i略去不写,如ali只写成al。
”后的式子中,各参量对应的下标i略去不写,如ali只写成al。
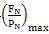
上述式中,ng表示工作推杆数。在没有顶切,又不修形的理论情况下,工作推杆数ng为推杆总数的一半。实际上,由于齿廓修形等原因,实际工作推杆数ng比理论情况下要少。
计算时,先根据输入功率P1及转速ωJ由(3.19)式计算出FJm,然后对每一工作推杆由式(3.17)计算出FJi,由式(3.10)式及式(3.11)计算出Fci及lci,最后代入式(3.21)计算出效率η。
当不考虑惯性力时,只需令上述公式中的Fr,FK,Fω都等于零,这时公式为:
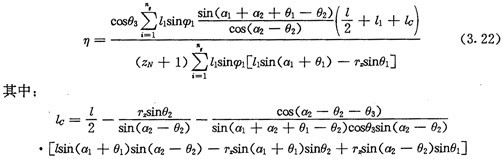
可见,在忽略惯性力影响的情况下,机构的啮合效率与输入功率、转速都无关。
从式(3.22)或式(3.21)可知,机构的整体啮合效率η与各工作推杆所对应的激波器位置角有关,而各工作推杆所对应的激波器位置角又可随啮合定位角 的确定被确定下来。因而,对指定的啮合定位角
的确定被确定下来。因而,对指定的啮合定位角 ,由式(3.22)可计算得到唯一的数值,当
,由式(3.22)可计算得到唯一的数值,当 在其取值范围内取不同值时,由式(3.22)所计算出的效率也略有不同。为此,将啮合定位角的取值区域[0,2π/ZC] 平均分成50等分,分别用式(3.22)计算啮合定位角取这50个位置的不同数值时机构的啮合效率,然后取其平均值作为机构的总平均啮合效率场,即
在其取值范围内取不同值时,由式(3.22)所计算出的效率也略有不同。为此,将啮合定位角的取值区域[0,2π/ZC] 平均分成50等分,分别用式(3.22)计算啮合定位角取这50个位置的不同数值时机构的啮合效率,然后取其平均值作为机构的总平均啮合效率场,即

对交点Q落在传动圈所在环外的情况,在方程组(3.9)中消去FN后,类似上述方法同样可求得此时的效率计算公式。实际计算表明,这种情况效率较低,而且推杆受力状态不好,将造成严重磨损。实际设计中应避免这种情况发生。因而在设计推杆减速器时,应正确选用传动圈尺寸及其它各参数,以确保Q点任何时候都能落在传动圈所在环内。
[算例]:
TW-3-16推杆减速器的参数是:Tb=50mm,Tz=6mm,e=3mm,l=22mm,ZN=15,ZC=16。
分析推杆减速器各啮合副的形式可知,推杆与导槽是滑动摩擦接触,激波器与内滚子可近似看作滚动摩擦接触,而内齿圈与外滚子之间滚滑两种成份都有。
由文献查得滑动摩擦系数为0.05-0.1,而滚动摩阻系数k=0.01mm,由文献可知滚动摩擦系数为k/Tz=0.0017。由于摩擦系数只是个参考数值,为了使计算结果更有实际意义,选用了三组不同摩擦系数的值,计算结果如表3.1所示。
表3.1选用不同摩擦角时啮合效率的计算结果
θ1 θ2 θ3 ηP
0.002 0.01 0.06 0.958
0.0025 0.015 0.07 0.951
0.003 0.02 0.08 0.946
设η机为推杆减速机的整体效率,ηZ为轴承效率,ηJ为工作时搅动润滑油的功率损失,则应有:
η机=ηP·ηZ·ηJ (3.24)
由试验知,η机=0.91,整机采用了4对轴承近似取ηZ=0.97,ηJ =0.98,由式(4.24)可得ηP=0.957。可见,实际啮合效与理论计算基本相符合。
3.3.3构件尺寸对啮合效率的影响
为了判断推杆减速器构件尺寸对其效率的影响,对3TWY7.5-12推杆减速器,选用同一组摩擦系数,而改变某一基本构件尺寸,并假定传动圈尺寸随之改变以确保受力交点Q落在传动圈所在环内,计算其啮合效率,结果如图3.7所示。
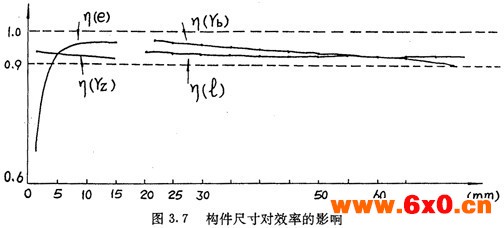
从图3.7可以看出,啮合效率随着激波器偏心距e的增大而升高,随着激波器半径Tb、滚子半径Tz、推杆长度l的增大而降低。其中偏心距。对效率的影响最为严重,推杆长度对效率的影响最小。
3.4强度校核
根据推杆减速器结构上的特点,强度校核应着重于各零件之间的接触强度。由于激波器与内滚子之间以及内齿圈与外滚子之间不仅相互作用力大,而且是线接触,因而这些零件是需要进行接触强度校核的主要对象。在推杆与传动圈导槽之间,由于接触面积较大,故接触应力不会太大。当零件所使用的材料及热处理方式不同时,其许用接触应力大小也不相同,因而对激波器与内滚子接触处以及内齿圈与外滚子接触处都应进行接触应力的计算。
3.4.1激波器与内滚子之间的接触应力
激波器与内滚子的接触,显然是两个圆柱体的相压接触,由弹性力学可知,在接触处产生的
最大接触应力σHJ可由下面的赫兹应力公式来计算:
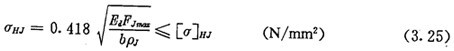
上式中:b为内滚子的工作长度。
Ed为当量弹性模量,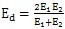 ,由于E1和E1都是钢材的弹性模量,所以Ed=E1=2.1×105
,由于E1和E1都是钢材的弹性模量,所以Ed=E1=2.1×105
N/mm2
PJ为当量曲率半径,PJ=
FJmax为激波器与内滚子之间的最大夺力,可近假用FJm来代替,由式(3.19)可得:
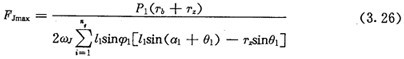
为求上式中的最大值,可将啮合定位角 在其取值范围内进行一维搜索。
在其取值范围内进行一维搜索。
[σ]HJ为激波器与内滚子所用材料的最小许用接触应力。
3.4.2内齿圈与外滚子之间的接触应力
由于内齿圈齿廓上各接触点都有对应的曲率,因此外滚子与内齿圈的接触,可看作是两个瞬时圆柱体的接触,在对应于内齿圈齿廓的齿顶部分,相当于两个圆柱体外接触,在对应于内齿圈齿廓的齿根部分,相当于两个圆柱体内接触。由于内齿圈理论齿廓曲线上各点的曲率半径不同,各点的作用力也不相等,因而在赫兹应力公式,需求出FN/PN的最大值,最大接触应力σHN为:

上式中k2为外滚子中心轨迹的相对曲率,在齿顶部分其值为正,在齿根部分其值为负。
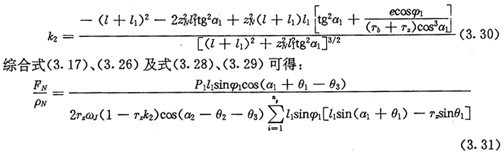
为求上式的最大值,首先给啮合定位角 在其取值范围内指定若干个离散点,对于
在其取值范围内指定若干个离散点,对于 在每个离散点上的取值,都分别计算出各工作推杆所应的FN/PN,取其中最大者。然后把
在每个离散点上的取值,都分别计算出各工作推杆所应的FN/PN,取其中最大者。然后把 取每个离散点时所对应的最大FN/PN再进行比较,可求得
取每个离散点时所对应的最大FN/PN再进行比较,可求得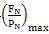 。
。










 QQ交流群
QQ交流群

